Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là sai?
-
A.
$I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2} + B{C^2}$
-
B.
$I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{D^2} + A{C^2}$
-
C.
$I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{E^2}$
-
D.
$I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2}$
Bước 1: Sử dụng tính chất hai cung bị chắn giữa hai dây song song thì bằng nhau để chứng minh $AC = ED$
Bước 2: Sử dụng định lý Pytago để chứng minh hệ thức.
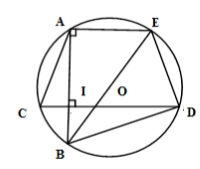
Xét $\left( O \right)$ có $BE$ là đường kính và $A \in \left( O \right)$$ \Rightarrow AE \bot AB$ mà $CD \bot AB$$ \Rightarrow AE{\rm{//}}CD$
Nên cung $AC$ bằng cung $ED$ hay $AC = ED$
Xét các tam giác vuông $\Delta IAC$ và $\Delta IBD$ ta có $I{A^2} + I{C^2} = A{C^2};I{B^2} + I{D^2} = B{D^2} $$\Rightarrow I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{C^2} + B{D^2} $$= E{D^2} + B{D^2}$
Mà $\Delta BED$ vuông tại $D$ nên $E{D^2} + B{D^2} = E{B^2}$
Hay $I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{E^2}$ nên C đúng mà \(BE \ne AD\) nên D sai.
Xét các tam giác vuông $\Delta IAD$ và $\Delta IBC$ ta có
$I{A^2} + I{D^2} = A{D^2};I{B^2} + I{C^2} = B{C^2}$$ \Rightarrow I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2} + B{C^2}$
Vậy A, B, C đúng, D sai.
Đáp án : D
Các bài tập cùng chuyên đề
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là trung điểm của bán kính \(OA\). Dây \(CD\) vuông góc với \(OA\) tại $H$ . Tính số đo cung lớn \(CD.\)
Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.
a) Tính khoảng cách từ O đến đường thẳng AB.
b) Tính\(\tan \alpha \)nếu góc ở tâm chắn cung AB bằng \(2\alpha .\)
Tâm O của một đường tròn cách dây AB của nó một khoảng 3 cm. Tính bán kính của đường tròn (O), biết rằng dây cung nhỏ AB có số đo bằng \(100^\circ \)(làm tròn kết quả đến hàng phần mười).
Cho tam giác ABC có hai đường cao BB’ và CC’. Gọi O là trung điểm BC.
a) Chứng minh đường tròn tâm O bán kính OB’ đi qua B, C, C’;
b) So sánh độ dài hai đoạn thẳng BC và B’C’.
Cho tứ giác ABCD có \(\widehat B = \widehat D = {90^o}\).
a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.
b) So sánh độ dài của AC và BD.
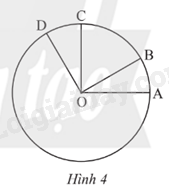
Quan sát Hình 4. Biết \(\widehat {DOA} = {120^o}\), OA \( \bot \)OC, OB \( \bot \)OD.
a) Đọc tên các góc ở tâm có trong hình.
b) Tính số đo của mỗi góc ở tâm tìm được ở câu a
c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180o
d) So sánh hai cung nhỏ \(\overset\frown{AB}\) và \(\overset\frown{CD}\).
Cho đường tròn tâm O và AB là một dây không đi qua tâm của (O). Gọi M là trung điểm của đoạn thẳng AB.
a) Chứng minh rằng OM vuông góc với AB.
b) Biết bán kính của đường tròn (O) là 10cm và \(OM = 6cm\), tính độ dài dây AB.
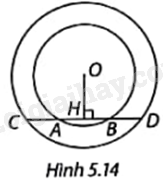
Trong Hình 5.14, cho hai đường tròn cùng tâm O, các điểm A, B, C, D thẳng hàng và \(OH \bot AB\left( {H \in AB} \right)\).
a) Chứng minh rằng H là trung điểm của AB và CD.
b) Chứng minh rằng \(AC = BD\).
c) Biết bán kính đường tròn lớn là 10cm, \(CD = 16cm\) và \(AB = 8cm\). Tính bán kính đường tròn nhỏ.
Cho điểm A thuộc đường tròn (O). Trên tiếp tuyến tại A của (O) xác định điểm M sao cho \(AM = AO\). Đường thẳng OM cắt (O) tại B và C (B nằm giữa O và M).
a) Tính góc ở tâm BOA.
b) Tính số đo cung lớn AC.
Góc nội tiếp chắn cung nhỏ AB có số đo \({55^o}\). Số đo của cung lớn AB là
A. \({55^o}\).
B. \({110^o}\).
C. \({205^o}\).
D. \({250^o}\).
Cho đường tròn (O;R) có dây AB = R. Số đo góc ở tâm \(\widehat {AOB}\) và cung lớn AB là:
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là điểm thuộc bán kính \(OA\) sao cho \(OH = \dfrac{{\sqrt 3 }}{2}OA\) . Dây \(CD\) vuông góc với \(OA\) tại $H.$ Tính số đo cung lớn \(CD.\)
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 55^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 60^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là sai?
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 3 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 2 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là đúng?
Một chiếc pizza hình tròn được chia thành 8 miếng như nhau bởi 4 nhát cắt qua tâm (H.5.6).
a) Mỗi miếng bánh có dạng một hình quạt tròn ứng với cung bao nhiêu độ?
b) Người ta chọn một chiếc hộp có đáy là hình vuông để đặt lọt chiếc bánh vào trong đó (mà vẫn giữ nguyên hình tròn). Hỏi mỗi cạnh đáy của chiếc hộp đó tối thiểu phải dài bao nhiêu centimét (làm tròn đến hàng đơn vị), biết rằng diện tích bề mặt mỗi miếng bánh đó bằng \(60c{m^2}\)?
Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’). So sánh độ dài dây BC của đường tròn (O) và độ dài dây BD của đường tròn (O’)
