Bát giác đều ABCDEFGH nội tiếp đường tròn bán kính bằng 1. Tính độ dài cạnh AB của bát giác.

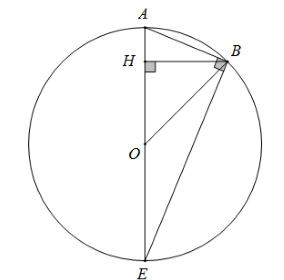
Vì ABCDEFGH là bát giác đều nên góc AOB bằng \(\dfrac{{360^\circ }}{8} = 45^\circ \) và AE là đường kính của đường tròn (O) ngoại tiếp bát giác.

Vẽ BH ⊥ AO tại H thì tam giác BHO vuông cân tại H (vì có góc BOH bằng \(45^0\).

Theo định lý Pytago ta có \(B{H^2} + O{H^2} = O{B^2}\)\( \Leftrightarrow 2B{H^2} = O{B^2} \)\(\Leftrightarrow BH = \dfrac{{OB}}{{\sqrt 2 }}\)

Suy ra

$\begin{array}{l}BH = OH = \dfrac{{OB}}{{\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}\\AH = AO - OH = 1 - \dfrac{1}{{\sqrt 2 }}\\AE = 2AO = 2\end{array}$

Vì AE là đường kính của (O) nên ∆ ABE vuông tại B, áp dụng hệ thức lượng trong tam giác vuông ta có

$A{B^2} = AH.AE = \left( {1 - \dfrac{1}{{\sqrt 2 }}} \right).2 = 2 - \sqrt 2 $

$ \Rightarrow AB = \sqrt {2 - \sqrt 2 } $