Hạt prôtôn p có động năng K1 = 5,48 MeV được bắn vào hạt nhân \({}_4^9Be\) đứng yên thì thấy tạo thành một hạt nhân \({}_3^6Li\) và một hạt X bay ra với động năng bằng K2 = 4MeV theo hướng vuông góc với hướng chuyển động của hạt p tới. Tính vận tốc chuyển động của hạt nhân Li (lấy khối lượng các hạt nhân tính theo đơn vị u gần bằng số khối). Cho 1 u = 931,5 MeV/c2.
-
A.
10,7.106 m/s
-
B.
1,07.106 m/s
-
C.
8,24.106 m/s
-
D.
0,824.106 m/s
Phương trình phản ứng hạt nhân: p + \({}_4^9Be\) \( \to \) \(\alpha \) + \({}_3^6Li\).
- Sử dụng công thức định luật bảo toàn động lượng: \(\overrightarrow {{p_p}} = \overrightarrow {{p_\alpha }} + \overrightarrow {{p_{Li}}} \)
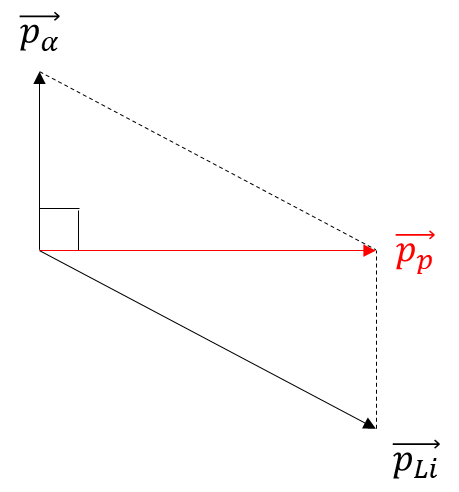
Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{p_p}} = \overrightarrow {{p_\alpha }} + \overrightarrow {{p_{Li}}} \) ta có hình vẽ:
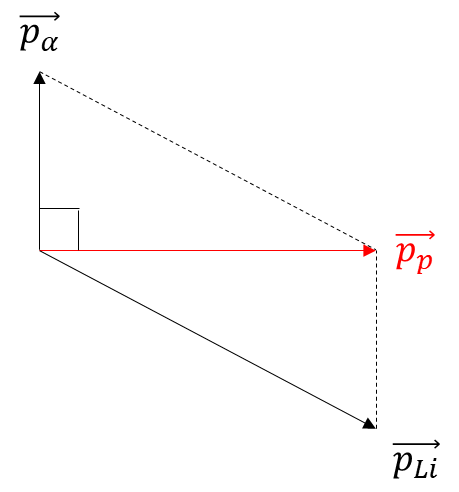
\( \to {p_{Li}}^2 = {p_\alpha }^2 + {p_p}^2\)
\( \to 2{m_{Li}}{K_{Li}} = 2{m_\alpha }{K_\alpha } + 2{m_p}{K_p}\)
\( \to {K_{Li}} = \dfrac{{{m_\alpha }{K_\alpha } + {m_p}{K_p}}}{{{m_{Li}}}} = \dfrac{{4.4 + 1.5,48}}{6} = 3,58MeV\)
Mà \({K_{Li}} = \dfrac{1}{2}{m_{Li}}{v_{Li}}^2 \to {v_{Li}} = \sqrt {\dfrac{{2{K_{Li}}}}{{{m_{Li}}}}} = \sqrt {\dfrac{{{{2.3,58.1,6.10}^{ - 13}}}}{{{{6.1,66055.10}^{ - 27}}}}} = {10,7.10^6}m/s\)
Đáp án : A
