Dùng p có động năng K₁ bắn vào hạt nhân \({}_4^9Be\) đứng yên gây ra phản ứng: \(p+{}_4^9Be \to \alpha + {}_3^6Li\). Phản ứng này thu năng lượng bằng 2,125MeV. Hạt nhân \({}_3^6Li\) và hạt α bay ra với các động năng lần lượt bằng K₂ = 4MeV và K₃ = 3,575MeV (lấy gần đúng khối lượng các hạt nhân, tính theo đơn vị u, bằng số khối). 1u = 931,5MeV/c². Góc giữa hướng chuyển động của hạt  α  và p bằng

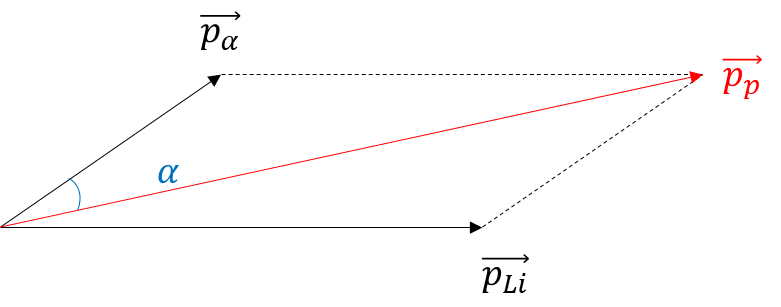
Phương trình phản ứng hạt nhân: p + \({}_4^9Be\) \( \to \) \(\alpha \) + \({}_3^6Li\).

- Ta có: Phản ứng này thu năng lượng bằng 2,125MeV \( \to \Delta E =  - 2,125MeV\)

- Mà \(\Delta E = {K_\alpha } + {K_{Li}} - {K_p} \to {K_p} = {K_\alpha } + {K_{Li}} - \Delta E = 4 + 3,575 - ( - 2,125) = 9,7MeV\)

Lại có: \(\overrightarrow {{p_p}}  = \overrightarrow {{p_\alpha }}  + \overrightarrow {{p_{Li}}} \)(Định luật bảo toàn động lượng)

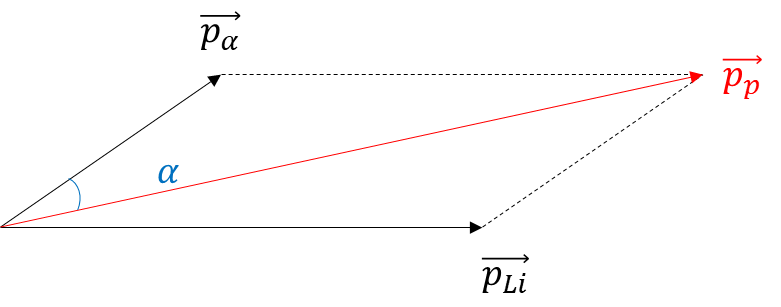
Từ hình vẽ, ta suy ra:

\( \to {p_{Li}}^2 = {p_\alpha }^2 + {p_p}^2 - 2{p_\alpha }{p_p}.cos\alpha \)

\( \to 2{m_{Li}}{K_{Li}} = 2{m_\alpha }{K_\alpha } + 2{m_p}{K_p} - 2.2{m_\alpha }{K_\alpha }.2{m_p}{K_p}.cos\alpha \)

\( \to {m_{Li}}{K_{Li}} = {m_\alpha }{K_\alpha } + {m_p}{K_p} - 4\sqrt {{m_\alpha }{K_\alpha }.{m_p}{K_p}} .cos\alpha \)

\( \to 6.4 = 4.3,575 + 1.9,7 - 4.\sqrt {4.3,575.1.9,7} .cos\alpha \)

\( \to cos\alpha  = 0 \to \alpha  = {90^0}\)