Đồ thị biểu diễn cường độ tức thời của dòng điện xoay chiều chỉ có cuộn cảm thuần có cảm kháng \(Z_L=50\Omega\) như hình sau:
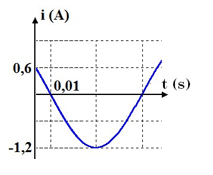
Viết biểu thức điện áp tức thời giữa hai đầu cuộn cảm.
-
A.
\(u = 60c{\rm{os(}}\dfrac{{50\pi t}}{3} + \dfrac{4\pi }{3})\)
-
B.
\(u = 60\sin {\rm{(}}\dfrac{{50\pi t}}{3} + \dfrac{4\pi }{3})\)
-
C.
\(u = 60c{\rm{os(}}\dfrac{{50\pi t}}{3} + \dfrac{\pi }{6})\)
-
D.
\(u = 30c{\rm{os(}}\dfrac{{50\pi t}}{3} + \dfrac{\pi }{3})\)
+ Đọc đồ thị cường độ dòng điện theo thời gian
+ Sử dụng công thức lượng giác: \({\rm{cos}}\left( x \right) = \sin \left( {x + \frac{\pi }{2}} \right)\)
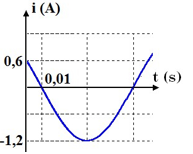
Từ đồ thị ta có:
\(\dfrac{T}{{12}} = 0,01{\rm{s}} \to T = 0,12{\rm{s}} \\\to \omega {\rm{ = }}\dfrac{{2\pi }}{T} = \dfrac{{50\pi }}{3}(ra{\rm{d}}/s)\)
+ Cường độ dòng điện cực đại:
\({I_0} = 1,2(A)\)
+ Tại \(t = 0\): \(i = 0,6A\) và đang giảm:
\(i = 0,6 \leftrightarrow {I_0}{\rm{cos}}\varphi {\rm{ = 0}}{\rm{,6}} \\\to c{\rm{os}}\varphi {\rm{ = }}\dfrac{{0,6}}{{1,2}} = \dfrac{1}{2} \to \varphi {\rm{ = }}\dfrac{\pi }{3}\)
=> Biểu thức cường độ dòng điện tức thời:
\(i = 1,2c{\rm{os}}\left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3}} \right)A\)
+ Ta có uL nhanh pha hơn i một góc \(\dfrac{\pi }{2}\)
+ Hiệu điện thế cực đại:
\({U_0} = {I_0}.{Z_L} = 1,2.50 = 60(V)\)
=> Biểu thức điện áp tức thời giữa hai đầu cuộn cảm:
$u = 60c{\rm{os}}\left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3} + \dfrac{\pi }{2}} \right) \\= 60\sin \left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3} + \dfrac{\pi }{2} + \dfrac{\pi }{2}} \right) \\= 60\sin \left( {\dfrac{{50\pi }}{3}t + \dfrac{{4\pi }}{3}} \right)V$
Đáp án : B








Danh sách bình luận