Đề bài
Tìm số tự nhiên a lớn nhất biết: $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$
-
A.
$125$
-
B.
$25$
-
C.
$175$
-
D.
$35$
Phương pháp giải
Ta đưa về bài toán tìm $ƯCLN$ của $525; 875; 280.$
Bước 1: Phân tích $525; 875; 280$ ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số nguyên tố chung đó, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Đó chính là số cần tìm.
Lời giải của GV Loigiaihay.com
Vì $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$ và $a$ là số lớn nhất$ \Rightarrow a = ƯCLN\left( {525;{\rm{ }}875;{\rm{ }}280} \right)$
Ta có:
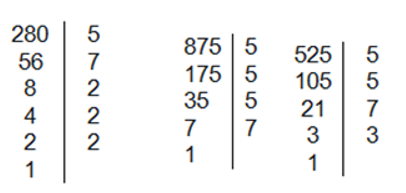
Nên \(525 = {3.5^2}.7;875 = {5^3}.7;280 = {2^3}.5.7\)
$ \Rightarrow \;a = $ ƯCLN$\left( {525;875;280} \right) = 5.7 = 35\;$
Đáp án : D
