Nếu tia phản xạ và tia khúc xạ vuông góc với nhau, mặt khác góc tới bằng \({60^0}\) thì chiết suất tỉ đối giữa môi trường khúc xạ và môi trường tới là :
-
A.
\(0,58\)
-
B.
\(0,71\)
-
C.
\(1,73\)
-
D.
\(1,33\)
+ Sử dụng biểu thức định luật khúc xạ ánh sáng: \(\dfrac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = {n_{21}} = \dfrac{{{n_2}}}{{{n_1}}} = n\)
+ Sử dụng mối quan hệ lượng giác của hai góc phụ nhau: \(i + r = {90^0} \to {\mathop{\rm s}\nolimits} {\rm{inr}} = c{\rm{osi}}\)
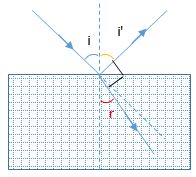
Ta có: tia phản xạ và tia khúc xạ vuông góc với nhau => \(i'{\rm{ + }}r{\rm{ = }}{90^0}\)
Mà \(i'{\rm{ = i}}\)=> \(i{\rm{ + }}r{\rm{ = }}{90^0}\)
+ Áp dụng định luật khúc xạ ánh sáng, ta được:
\(\dfrac{{{\rm{Sin i}}}}{{{\rm{Sin r}}}}{\rm{ = }}{{\rm{n}}_{{\rm{21}}}}{\rm{ = }}\dfrac{{{{\rm{n}}_{\rm{2}}}}}{{{{\rm{n}}_{\rm{1}}}}} = {\rm{n}}\) (1)
+ Mặt khác, ta có: \({\rm{i + r = 9}}{{\rm{0}}^{\rm{0}}} \to s{\rm{in r = cos i}}\)(2)
Từ (1) và (2), ta suy ra: \(tani = n \to n = \tan {60^0} \to n \sim 1,73\)
Đáp án : C
Các bài tập cùng chuyên đề
Phát biểu nào sau đây là đúng?
Với một tia sáng đơn sắc, chiết suất tuyệt đối của nước là \({n_1}\), của thủy tinh là \({n_2}\). Chiết suất tỉ đối khi tia sáng đó truyền từ nước sang thủy tinh là:
Khi có hiện tượng phản xạ thì tia tới và tia phản xạ
Trong hiện tượng khúc xạ ánh sáng
Khi xảy ra hiện tượng khúc xạ ánh sáng thì quan hệ giữa góc tới và góc khúc xạ tuân theo quy luật:
Chiết suất tỉ đối giữa môi trường khúc xạ với môi trường tới
Khi ánh sáng truyền từ môi trường 1 sang môi trường 2 thì ta sẽ nói môi trường 2 kém chiết quang hơn môi trường 1 nếu chiết suất tỉ đối:
Khi tia sáng đi từ môi trường trong suốt \({n_1}\) tới mặt phân cách với môi trường trong suốt \({n_2}\) (với \({n_2} > {n_1}\)), tia sáng không vuông góc với mặt phân cách thì:
Nếu giữa không khí và nước có \(n = \dfrac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \dfrac{4}{3}\) thì người ta gọi \(\dfrac{4}{3}\) là chiết suất tỉ đối của
Chiếu một tia sáng đơn sắc đi từ không khí vào môi trường có chiết suất \(n\), sao cho tia phản xạ vuông góc với tia khúc xạ. Khi đó góc tới \(i\) được tính theo công thức:
Một tia sáng truyền từ không khí tới bề mặt một môi trường trong suốt sao cho tia phản xạ và tia khúc xạ vuông góc nhau. Khi đó góc tới và góc khúc xạ liên hệ với nhau qua hệ thức :
Một tia sáng truyền từ không khí tới bề mặt môi trường trong suốt chiết suất \(n = \sqrt 3 \) sao cho tia phản xạ và tia khúc xạ vuông góc nhau. Khi đó góc tới \(i\) có giá trị là:
Một điểm sáng \(S\) nằm trong chất lỏng chiết suất n, cách mặt chất lỏng một khoảng \(12{\rm{ }}cm\), phát ra chùm sáng hẹp đến gặp mặt phân cách tại điểm \(I\) với góc tới rất nhỏ, tia ló truyền theo phương \(IR\). Đặt mắt trên phương \(IR\) nhìn thấy ảnh ảo \(S'\) của \(S\) dường như cách mặt chất lỏng một khoảng \(10{\rm{ }}cm\). Chiết suất của chất lỏng đó là:
Một người nhìn hòn sỏi dưới đáy một bể nước thấy ảnh của nó dường như cách mặt nước một khoảng \(1,2m\), chiết suất của nước là \(n = \dfrac{4}{3}\). Độ sâu của bể là:
Một người nhìn xuống đáy một chậu nước. Chiều cao của lớp nước trong chậu là \(20{\rm{ }}cm\). Người đó thấy đáy chậu dường như cách mặt nước một khoảng bằng bao nhiêu? Biết chiết suất của nước là \(\dfrac{4}{3}\)
Phát biểu nào sau đây là không đúng?
Khi một chùm tia sáng phản xạ toàn phần tại mặt phân cách giữa hai môi trường thì:
Phát biểu nào sau đây là không đúng?
Khi ánh sáng đi từ nước có chiết suất \(n = \dfrac{4}{3}\) sang không khí, góc giới hạn phản xạ toàn phần có giá trị là:
Tia sáng đi từ thủy tinh \(\left( {{n_1} = 1,5} \right)\) đến mặt phân cách với nước \(\left( {{n_2} = \dfrac{4}{3}} \right)\). Điều kiện của góc tới \(i\) để không có tia khúc xạ trong nước là:
