Đề bài
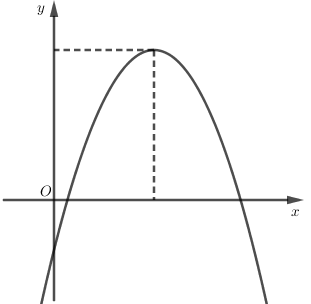
Cho hàm số $y = a{x^2} + bx + c$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
-
A.
$a < 0$, $b < 0$, $c < 0$.
-
B.
$a < 0$, $b = 0$, $c < 0$.
-
C.
$a > 0$, $b > 0$, $c < 0$.
-
D.
$a < 0$, $b > 0$, $c < 0$.
Phương pháp giải
Quan sát đồ thị hàm số, nhận xét đỉnh parabol, dáng bề lõm và điểm đi qua, từ đó suy ra \(a,b,c\)
Lời giải của GV Loigiaihay.com
Quan sát đồ thị ta có:
Đồ thị quay bề lõm xuống dưới nên \(a < 0\); có hoành độ đỉnh \({x_I} = - \dfrac{b}{{2a}} > 0 \Leftrightarrow \dfrac{b}{a} < 0 \Rightarrow b > 0\).
Lại có: đồ thị cắt \(Oy\) tại điểm có tung độ âm nên \(c < 0\).
Vậy $a < 0$, $b > 0$, $c < 0$.
Đáp án : D
Chú ý
Một số em có thể sẽ chọn nhầm A vì ở bước xét $ - \dfrac{b}{{2a}} > 0$ lại suy ra $b<0$ là sai.
Danh sách bình luận