Cho các tập hợp khác rỗng \(A=\left[ {m - 1;\dfrac{{m + 3}}{2}} \right]\) và \(B = \left( { - \infty ; - 3} \right) \cup \left[ {3; + \infty } \right)\). Tập hợp các giá trị thực của \(m\) để \(A \cap B \ne \emptyset \) là
-
A.
\(\left( { - \infty ; - 2} \right) \cup \left[ {3; 5 } \right)\).
-
B.
\(\left( { - 2;3} \right)\).
-
C.
$\left( { - \infty ; - 2} \right) \cup \left[ {3;5} \right]$.
-
D.
\(\left( { - \infty ; - 9} \right) \cup \left( {4; + \infty } \right)\).
Hai tập hợp có giao khác rỗng nếu chúng có ít nhất \(1\) điểm chung.
Để \(A \cap B \ne \emptyset \) thì điều kiện là \(\left\{ \begin{array}{l}m - 1 \le \dfrac{{m + 3}}{2}\\\left[ \begin{array}{l}m - 1 < - 3\\\dfrac{{m + 3}}{2} \ge 3\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 5\\\left[ \begin{array}{l}m < - 2\\m \ge 3\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m \le 5\\m < - 2\end{array} \right.\\\left\{ \begin{array}{l}m \le 5\\m \ge 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < - 2\\3 \le m \le 5\end{array} \right.\).
Vậy \(m \in \left( { - \infty - 2} \right) \cup \left[ {3;5} \right]\)
Minh họa bằng trục số
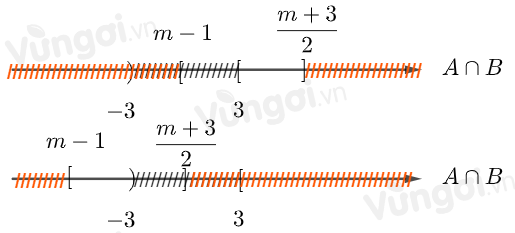
Đáp án : C
+ Một số em có thể sẽ quên mất trường hợp \(m = 5\) và chọn đáp án A là sai.
+ Các em cũng có thể làm theo phương pháp phần bù, tìm điều kiện để hai tập giao nhau bằng rỗng (hoặc tập \(A\) không tồn tại) rồi lấy phần bù của nó trong \(\mathbb{R}\)








Danh sách bình luận