Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\); \(SA = a\) đáy \(ABC\) là tam giác vuông tại \(B\), \(\widehat {BAC} = 60^\circ \) và \(AB = \dfrac{a}{2}\). Gọi \(\left( S \right)\) là mặt cầu ngoại tiếp hình chóp \(S.ABC\). Tìm mệnh đề sai.
-
A.
Diện tích của \(\left( S \right)\) là \(\dfrac{{2\pi {a^2}}}{3}\).
-
B.
Tâm của \(\left( S \right)\) là trung điểm \(SC\).
-
C.
\(\left( S \right)\) có bán kính $\dfrac{{a\sqrt 2 }}{2}$.
-
D.
Thể tích khối cầu là \(\dfrac{{\sqrt 2 \pi {a^3}}}{3}\).
- Xác định tâm mặt cầu (cách đều \(4\) đỉnh hình chóp)
- Tính bán kính rồi suy ra các giá trị diện tích, thể tích và kết luận đáp án đúng.
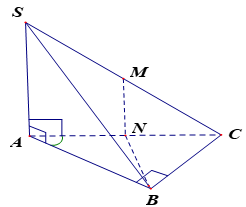
Gọi \(N,\,M\) lần lượt là trung điểm của \(AC;\,SC\).
\(ABC\) là tam giác vuông tại \(B\), \(\widehat {BAC} = {60^o}\) và \(AB = \dfrac{a}{2}\) nên \(NA = NB = NC\); \(AC = a \Rightarrow SC = a\sqrt 2 \Rightarrow MC = \dfrac{{a\sqrt 2 }}{2}\).
\(NM\) là đường trung bình của tam giác \(SAC\) nên \(NM//SA \Rightarrow NM \bot \left( {ABC} \right)\, \Rightarrow \,\,{\rm{MS = MC = MA = MB}}\)
\( \Rightarrow \) $M$ là tâm của \(\left( S \right)\) có bán kính \(MC = \dfrac{{a\sqrt 2 }}{2}\).
\( \Rightarrow {V_{{}_{\left( S \right)}}} = \dfrac{4}{3}\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^3} = \dfrac{{\sqrt 2 \pi {a^3}}}{3}\).
Diện tích của \(\left( S \right):\,S = 4\pi {r^2} = 4\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} = 2\pi {a^2}.\)
Đáp án : A








Danh sách bình luận