Đề bài
Cho hình vẽ ở bên. Biết \( \widehat {BAx}=20^0\).
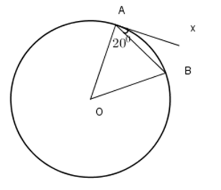
Hãy tính số đo của cung bị chắn \(AB.\)
-
A.
\({100^0}\)
-
B.
\({60^0}\)
-
C.
\({80^0}\)
-
D.
\({40^0}\)
Phương pháp giải
Sử dụng góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn
Lời giải của GV Loigiaihay.com
Do \(Ax\) là tiếp tuyến với \(\left( O \right)\) tại \(A\) nên \(\widehat {BAx} = \dfrac{1}{2}\) sđ\(\overparen{AB}\)
hay sđ \(\overparen{AB}= 2\widehat {BAx} = {2.20^0} = {40^0}\)
Vì vậy sđ\(\overparen{AB} = {40^0}.\)
Đáp án : D







