Cho tam giác \(ABC\) cân tại \(A\) nội tiếp đường tròn tâm \(O.\) Trên \(\left( O \right)\) lấy điểm \(D\) thuộc cung \(AC\). Gọi \(E = AC \cap BD,\,\,F = AD \cap BC.\) Khi đó mệnh đề đúng là:
-
A.
\(\widehat {AFB} > \widehat {ABD}\)
-
B.
\(\widehat {AFB} < \widehat {ABD}\)
-
C.
\(\widehat {AFB} = 2\widehat {ABD}\)
-
D.
\(\widehat {AFB} = \widehat {ABD}\)
Áp dụng tính chất góc nội tiếp, góc có đỉnh nằm ngoài đường tròn, các cung chắn hai dây bằng nhau để chứng minh \(\widehat {AFB} = \widehat {ABD}.\)
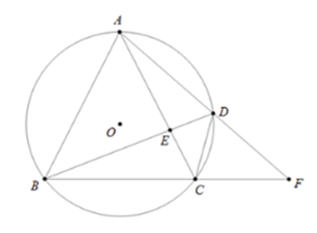
\(\Delta ABC\) cân tại \(A\) nên \(AB = AC\) suy ra \(sđ\,\overparen{AB} = sđ\,\overparen{AC}.\)
Áp dụng kết quả trên và theo tính chất của góc ngoài đường tròn ta có:
$\widehat {AFB} = \dfrac{1}{2}\left( {sđ\,\overparen{AB} - sđ\,\overparen{CD}} \right) = \dfrac{1}{2}\left( {sđ\,\overparen{AC} - sđ\,\overparen{CD}} \right) = \dfrac{1}{2}sđ\,\overparen{AD}.$
Mặt khác theo tính chất góc nội tiếp ta có \(\widehat {ABD} = \dfrac{1}{2}sđ\,\overparen{AD}.\)
Do đó \(\widehat {AFB} = \widehat {ABD}.\)
Đáp án : D







