Cho hình vuông nội tiếp đường tròn $\left( {O;R} \right)$. Chu vi của hình vuông là
-
A.
$2R\sqrt 2 $
-
B.
$3R\sqrt 2 $
-
C.
$4R\sqrt 2 $
-
D.
$6R$
Xác định đường kính của đường tròn
Định lí Py-ta-go
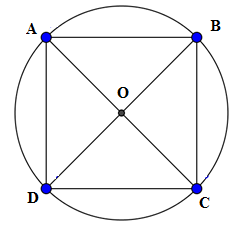
Hình vuông \(ABCD\) nội tiếp đường tròn tâm \(O.\)
Khi đó đường chéo \(BD\) là đường kính của \(\left( O \right)\)
Suy ra \(BD = 2R\)
Xét tam giác \(BDC\) vuông cân tại \(C,\) theo định lý Pytago ta có
$B{C^2} + C{D^2} = B{D^2} \Leftrightarrow 2B{C^2} = 4{R^2} \Rightarrow BC = R\sqrt 2 $
Chu vi hình vuông \(ABCD\) là \(4R\sqrt 2 \)
Đáp án : C
Kẻ $OE \bot BC\left( {E \in \left( {O;R} \right)} \right),OE \cap BC = \left\{ F \right\}$
Xét $\Delta OCF$ vuông tại $F$ nên theo định lí Pi-ta-go ta có $O{F^2} + C{F^2} = O{C^2} = {R^2}$.
Mà $OF = CF$ (vì cùng bằng nửa cạnh hình vuông)
Nên $2O{F^2} = {R^2} \Rightarrow OF = \dfrac{{R\sqrt 2 }}{2} \Rightarrow CD = 2OF = R\sqrt 2 $.
Chu vi hình vuông là $4R\sqrt 2 $.
