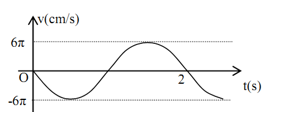
Đồ thị vận tốc của một vật cho ở hình bên, phương trình nào dưới đây là phương trình dao động của vật:
-
A.
\(x = 6c{\rm{os}}\left( {\pi t + \frac{\pi }{2}} \right)cm\)
-
B.
\(x = 6c{\rm{os}}\left( {\pi t} \right)cm\)
-
C.
\(x = 6c{\rm{os}}\left( {\pi t - \frac{\pi }{2}} \right)cm\)
-
D.
\(x = 6\sin \left( {\pi t} \right)cm\)
- Sử dụng phương pháp đọc đồ thị vận tốc theo thời gian của vật
+ Từ đồ thị xác định A, chu kì T, li độ và vận tốc tại thời điểm t = 0
Từ đồ thị, ta có: $T{\rm{ }} = {\rm{ }}2s \to \omega = \frac{{2\pi }}{T} = \pi ra{\rm{d}}/s$
$A\omega = 6\pi cm/s \to A = \frac{{6\pi }}{\omega } = \frac{{6\pi }}{\pi } = 6cm$
Tại t = 0: \({\rm{v = - A}}\omega {\rm{sin}}\varphi = 0 \to \sin \varphi = 0 \to \left[ \begin{array}{l}\varphi = 0\\\varphi = \pi \end{array} \right.\)
và đang đi theo chiều âm\( \to \varphi = 0\)
\( \Rightarrow x = 6c{\rm{os}}\left( {\pi t} \right)cm\)
Đáp án : B