Giải bất phương trình \({\log _{0,7}}\left( {{{\log }_6}\dfrac{{{x^2} + x}}{{x + 4}}} \right) < 0\)
-
A.
\(\left( { - 4; - 3} \right) \cup \left( {8; + \infty } \right)\)
-
B.
\(\left( { - 4; - 3} \right)\)
-
C.
\(\left( { - 4; + \infty } \right)\)
-
D.
\(\left( {8; + \infty } \right)\)
Giải bất phương trình logarit cơ bản với chú ý về cơ số $a>1$ và $0<a<1$.
${\log _{0,7}}({\log _6}\dfrac{{{x^2} + x}}{{x + 4}}) < 0$ .
Đkxđ: $\left\{ \begin{array}{l}{\log _6}\dfrac{{{x^2} + x}}{{x + 4}} > 0\\\dfrac{{{x^2} + x}}{{x + 4}} > 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 4 < x < - 2\\x > 2\end{array} \right.(*)$
\(\begin{array}{l}{\log _6}\dfrac{{{x^2} + x}}{{x + 4}} > 0,{7^0} = 1 \Leftrightarrow \dfrac{{{x^2} + x}}{{x + 4}} > 6 \Leftrightarrow \dfrac{{{x^2} + x}}{{x + 4}} - 6 > 0\\ \Leftrightarrow \dfrac{{{x^2} - 5{\rm{x}} - 24}}{{x + 4}} > 0 \Leftrightarrow \dfrac{{(x - 8)(x + 3)}}{{x + 4}} > 0\end{array}\)
Xét dấu \(f\left( x \right) = \dfrac{{(x - 8)(x + 3)}}{{x + 4}}\):
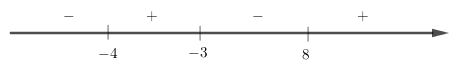
Vậy \( - 4 < x < - 3\) hoặc \(x > 8\).
Kết hợp với điều kiện ta được \( - 4 < x < - 3\) hoặc \(x > 8\).
Đáp án : A
