Tập nghiệm của bất phương trình $\ln\left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0$ là:
-
A.
$\left( {1;2} \right) \cup \left( {3; + \infty } \right)$
-
B.
$\left( { - \infty ;1} \right) \cup \left( {2;3} \right)$
-
C.
$\left( {1;2} \right) \cap \left( {3; + \infty } \right)$
-
D.
$\left( { - \infty ;1} \right) \cap \left( {2;3} \right)$
Tìm điều kiện để hàm $\ln f\left( x \right)$ có nghĩa là $f\left( x \right) > 0$,$\ln f(x) > 0 \Leftrightarrow f(x) > 1$ sau đó tìm $x$ .
$\begin{array}{l}\ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1 > 1\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) > 0\end{array}$
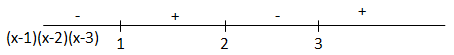
$ \Rightarrow x \in (1;2) \cup (3; + \infty )$
Đáp án : A
