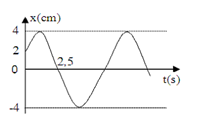
Một vật dao động điều hoà có đồ thị như hình vẽ.
Phương trình dao động của vật là:
-
A.
\(x = 4c{\rm{os}}\left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)cm\)
-
B.
\(x = 4c{\rm{os}}\left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right)cm\)
-
C.
\(x = 4c{\rm{os}}\left( {\pi t - \frac{\pi }{6}} \right)cm\)
-
D.
\(x = 4c{\rm{os}}\left( {\frac{{2\pi }}{3}t - \frac{{5\pi }}{6}} \right)cm\)
- Sử dụng phương pháp đọc đồ thị li độ theo thời gian của vật
+ Từ đồ thị xác định $A$, chu kì $T$, li độ và vận tốc tại thời điểm $t = 0$
Từ đồ thị, ta có: \(A{\text{ }} = {\text{ }}4cm\)
Thời gian vật đi từ \(t = 0{\text{ }}\left( {x = \frac{A}{2}} \right)\) đến \(t = 2,5s{\text{ }}\left( {x = 0} \right)\) là:
\(\Delta t = 2,5{\rm{s}} = \frac{T}{6} + \frac{T}{4} = \frac{{5T}}{{12}} \to T = 6{\rm{s}} \to \omega = \frac{{2\pi }}{T} = \frac{\pi }{3}ra{\rm{d}}/s\)
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 2\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = \frac{2}{4} = \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{3}\)
\( \Rightarrow x = 4c{\rm{os}}\left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)cm\)
Đáp án : A







