Đề bài
Cho ba số thực dương $a, b, c$ khác $1$. Đồ thị các hàm số $y = \log_{a} x, y=\log_{b} x, y= \log_{c} x$ được cho trong hình vẽ sau:
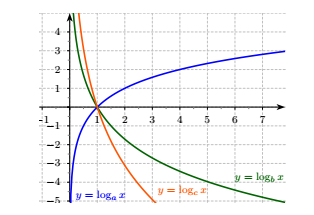
Mệnh đề nào dưới đây đúng?
-
A.
$a<b<c$
-
B.
$b<c<a $
-
C.
$a<c<b $
-
D.
$c<a<b$
Phương pháp giải
Quan sát hình vẽ và áp dụng tính chất đồng biến, nghịch biến của hàm số logarit.
Lời giải của GV Loigiaihay.com
Quan sát hình vẽ ta thấy:
- Hàm số \(y = {\log _a}x\) là hàm đồng biến nên ta có \(a > 1\) .
- Hai hàm số \(y = {\log _b}x,y = {\log _c}x\) nghịch biến nên có \(0 < b,c < 1\)
Từ nhận xét này ta thấy \(a\) là số lớn nhất.
Đáp án : B








Danh sách bình luận