Trong không gian với hệ tọa độ \(Oxyz,\left( \alpha \right)\) cắt mặt cầu $\left( S \right)$ tâm \(I\left( {1; - 3;3} \right)\) theo giao tuyến là đường tròn tâm \(H\left( {2;0;1} \right)\) , bán kính $r = 2$ . Phương trình (S) là:
-
A.
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 3} \right)^2} = 18\)
-
B.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 3} \right)^2} = 4\)
-
C.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 3} \right)^2} = 18\)
-
D.
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 3} \right)^2} = 4\)
+ Xác định bán kính mặt cầu $(S)$.
+Phương trình mặt cầu: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
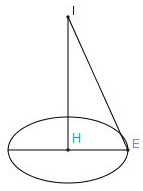
Gọi $E $ là một điểm thuộc đường tròn.
Ta có \(IH = d\left( {I,(\alpha)} \right);\,R = IE;\,r=HE\)
\(IH = \sqrt {1 + {3^2} + {(-2)^2}} = \sqrt {14} \)
Tam giác $IHE$ vuông tại $H$ nên \(IE = \sqrt {I{H^2} + H{E^2}} = \sqrt {14 + 4} = \sqrt {18} \)
Suy ra phương trình mặt cầu $(S)$ là:
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 3} \right)^2} = 18\).
Đáp án : A
