Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH$.
a) Chứng minh rằng $AB^{2} = BH.BC$.
b) Giả sử $AB = 3cm$, $BC = 5cm$. Giải tam giác vuông $ABH$ (kết quả số đo góc làm tròn đến phút).
c) Gọi $M,N$ lần lượt là hình chiếu của $H$ trên $AB,AC$. Chứng minh $\text{Δ}AMN$ đồng dạng với $\text{Δ}ACB$ và $S_{\text{Δ}ABC} = \dfrac{S_{\text{Δ}MHN}}{\text{cos}^{2}B\text{cos}^{2}C}$.
a) Chứng minh rằng $AB^{2} = BH.BC$.
Chứng minh $\Delta ABC \backsim \Delta HBA\left( {g.g} \right)$, suy ra $AB^{2} = BH.BC$.
b) Giải tam giác vuông $ABH$ (kết quả số đo góc làm tròn đến phút).
Từ $AB^{2} = BH.BC$ (cmt), tính $BH$.
Áp dụng định lí Pythagore vào tam giác ABH để tính AH.
Áp dụng tỉ số lượng giác trong tam giác ABH, tính góc B.
Từ đó suy ra số đo góc BAH.
$\sin B = \dfrac{AH}{AB} = \dfrac{12}{5}:3 = \dfrac{4}{5}$ nên $B \approx 53{^\circ}8'$.
c) * Chứng minh $\Delta AMN \backsim \Delta ACB$
Gọi I là giao điểm của MN và AH.
Chứng minh tứ giác AMHN là hình chữ nhật suy ra MN và AH cắt nhau tại trung điểm của mỗi đường, nên $\Delta MIA$ cân tại I, suy ra hai góc ở đáy bằng nhau.
Từ đó chứng minh $\Delta AMN \backsim \Delta ACB$ (g.g)
* Chứng minh $S_{\text{Δ}ABC} = \dfrac{S_{\text{Δ}MHN}}{\text{cos}^{2}B\text{cos}^{2}C}$
Dựa vào đặc điểm của hình chữ nhật và tính chất hai đường thẳng song song suy ra các cặp góc đồng vị bằng nhau,
Chứng minh $\Delta AMN = \Delta HNM$, dẫn đến $\Delta HMN \backsim \Delta ABC$.
Suy ra $\dfrac{S_{\Delta HMN}}{S_{\Delta ABC}} = \dfrac{HM.HN}{AB.AC}$
Nhân cả tử và mẫu với BH.HC, từ đó biến đổi về tỉ số lượng giác cosin của góc B, C để chứng minh $\dfrac{S_{\Delta HMN}}{S_{\Delta ABC}} = \cos^{2}B.\cos^{2}C$
Do đó $S_{\Delta ABC} = \dfrac{S_{\Delta MHN}}{\cos^{2}B.\cos^{2}C}$.
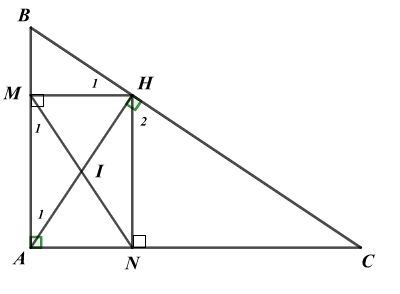
a) Chứng minh rằng $AB^{2} = BH.BC$.
Xét $\Delta ABC$ và $\Delta HBA$ có:
$\widehat{BAC} = \widehat{BHA}$ $\left( {= 90{^\circ}} \right)$
$\widehat{B}$ chung
Do đó $\Delta ABC \backsim \Delta HBA\left( {g.g} \right)$, suy ra $\dfrac{AB}{BC} = \dfrac{BH}{AB}$ nên $AB^{2} = BH.BC$.
b) Giả sử $AB = 3cm$, $BC = 5cm$. Giải tam giác vuông $ABH$ (kết quả số đo góc làm tròn đến phút).
Vì $AB^{2} = BH.BC$ (cmt) nên $BH = \dfrac{AB^{2}}{BC} = \dfrac{3^{2}}{5} = \dfrac{9}{5}\left( {cm} \right)$.
Áp dụng định lí Pythagore vào tam giác ABH, ta có:
$AH^{2} = AB^{2} - BH^{2} = 3^{2} - \left( \dfrac{9}{5} \right)^{2} = \dfrac{144}{25}$, suy ra $AH = \sqrt{\dfrac{144}{25}} = \dfrac{12}{5}\left( {cm} \right)$.
Áp dụng tỉ số lượng giác trong tam giác ABH, ta có:
$\sin B = \dfrac{AH}{AB} = \dfrac{12}{5}:3 = \dfrac{4}{5}$ nên $B \approx 53{^\circ}8'$.
Suy ra $\widehat{BAH} = 90{^\circ} - 53{^\circ}8' = 36{^\circ}52'$.
Vậy $AH = \dfrac{12}{5}cm,BH = \dfrac{9}{5}cm,AB = 3cm$, $\widehat{AHB} = 90{^\circ},\widehat{ABH} = 53{^\circ}8',\widehat{BAH} = 36{^\circ}52'$,
c) Gọi $M,N$ lần lượt là hình chiếu của $H$ trên $AB,AC$. Chứng minh $\text{Δ}AMN$ đồng dạng với $\text{Δ}ACB$ và $S_{\text{Δ}ABC} = \dfrac{S_{\text{Δ}MHN}}{\text{cos}^{2}B\text{cos}^{2}C}$.
* Chứng minh $\Delta AMN \backsim \Delta ACB$
Gọi I là giao điểm của MN và AH.
Xét tứ giác AMHN có:
$\widehat{MAN} = 90{^\circ}$ (gt)
$\widehat{AMH} = \widehat{ANH}$ (do $M,N$ lần lượt là hình chiếu của $H$ trên $AB,AC$)
nên tứ giác AMHN là hình chữ nhật.
Suy ra MN và AH cắt nhau tại trung điểm của mỗi đường, do đó MI = IH = IN = IA, suy ra $\Delta MIA$ cân tại I, suy ra $\widehat{M_{1}} = \widehat{A_{1}}$ (tính chất tam giác cân).
Mà $\widehat{A_{1}} + \widehat{B} = 90{^\circ}$, $\widehat{B} + \widehat{C} = 90{^\circ}$ nên $\widehat{A_{1}} = \widehat{C}$, suy ra $\widehat{M_{1}} = \widehat{C}$
Xét $\Delta AMN$ và $\Delta ACB$ có:
$\widehat{BAC}$ chung
$\widehat{M_{1}} = \widehat{C}$
Do đó $\Delta AMN \backsim \Delta ACB$ (g.g)
* Chứng minh $S_{\text{Δ}ABC} = \dfrac{S_{\text{Δ}MHN}}{\text{cos}^{2}B\text{cos}^{2}C}$
Vì AMHN là hình chữ nhật nên MH // AC và NH // AB, suy ra $\widehat{H_{1}} = \widehat{C},\widehat{H_{2}} = \widehat{B}$
Xét $\Delta AMN$ và $\Delta HNM$ có:
$AM = HN$ (vì AMHN là hình chữ nhật)
$\widehat{MAB} = \widehat{NHM}\left( {= 90{^\circ}} \right)$
$AN = HM$ (vì AMHN là hình chữ nhật)
nên $\Delta AMN = \Delta HNM$.
Mà $\Delta AMN \backsim \Delta ACB$, suy ra $\Delta HMN \backsim \Delta ABC$.
Suy ra $\dfrac{S_{\Delta HMN}}{S_{\Delta ABC}} = \dfrac{HM.HN}{AB.AC}$
$\begin{array}{l} {= \dfrac{HM.BH.HN.HC}{BH.AB.HC.AC}} \\ {= \dfrac{HM}{BH}.\dfrac{BH}{AB}.\dfrac{HN}{HC}.\dfrac{HC}{AC}} \\ {= \cos H_{1}.\cos B.\cos H_{2}.\cos C} \\ {= \cos C.\cos B.\cos B.\cos C} \\ {= \cos^{2}B.\cos^{2}C} \end{array}$
Do đó $S_{\Delta ABC} = \dfrac{S_{\Delta MHN}}{\cos^{2}B.\cos^{2}C}$.

Các bài tập cùng chuyên đề
Một khúc sông rộng khoảng $250m$. Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên, nên phải đi khoảng $320m$ mới sang được bờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một góc bao nhiêu độ?
-
A.
$30^\circ $
-
B.
$40^\circ $
-
C.
$38^\circ 37'$
-
D.
$39^\circ 37'$
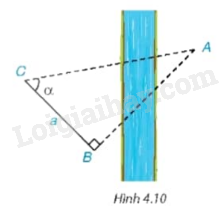
Để tính khoảng cách giữa hai địa điểm A, B không đo trực tiếp được, chẳng hạn A và B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho tam giác ABC vuông tại B. Ở bên bờ sông chứa B, người ta đo được \(\widehat {ACB} = \alpha \) và \(BC = a\) (H.4.10) . Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết \(\alpha = {55^0},a = 70\) m.
Trở lại bài toán ở tình huống mở đầu: Trong một toàn chung cư, biết đoạn dốc vào sảnh toàn nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.
a) Hãy tính góc dốc.
b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?
Tình huống mở đầu:
Ta có thể xác định “góc dốc” \(\alpha \) của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1)
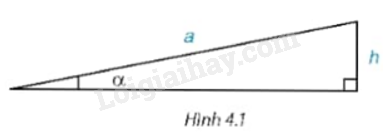
(Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn \({6^0}\)) .
Xét các tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại. Hỏi các tam giác đó có đồng dạng với nhau không? Tính sin và cos của góc nhọn lớn hơn.
a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):
22o
52o
15o20’
52o18’
b) Tìm các góc nhọn x, y, z, t trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm hoặc đến phút):
sin x = 0,723
cos y = 0,828
tan z = 3,77
cot t = 1,54.
a) Vẽ một tam giác vuông có góc bằng 40o . Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40o . Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.
b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thức đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau:
a) BC = 5 cm; AB = 3 cm.
b) BC = 13cm; AC = 12 cm
c) BC = \(5\sqrt 2 \) cm; AB = 5 cm
d) AB = \(a\sqrt 3 \); AC = a
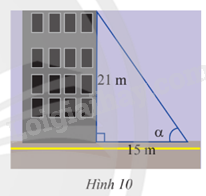
Tia nắng chiếu qua nóc của một tòa nhà hợp với mặt đất một góc\(\alpha \). Cho biết tòa nhà cao 21m và bóng của nó trên mặt đất dài 15m (Hình 10). Tính góc\(\alpha \) (kết quả làm tròn đến độ).
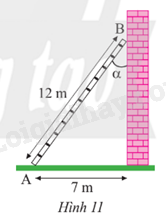
Một cái thang dài 12m được đặt dựa vào một bức tường sao cho chân thang cách tường 7m (Hình 11). Tính góc \(\alpha \) tạo bởi thang và tường.
Giá trị của biểu thức \(B = tan{20^o}.\tan {30^o}.\tan {40^o}.\tan {50^o}.\tan {60^o}.tan{70^o}\) là
A. 2
B. 1
C. 3
D. 4
Cho tam giác ABC vuông tại A có AB = 18 cm, AC = 24 cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.
Cho góc nhọn \(\alpha \) biết sin\(\alpha \) = 0,8. Tính cos\(\alpha \), tan \(\alpha \) và cot\(\alpha \).
Cho góc nhọn \(\alpha \). Biết rằng, tam giác \(ABC\) vuông tại \(A\) sao cho \(\widehat B = \alpha \).
a) Biểu diễn các tỉ số lượng giác của góc nhọn \(\alpha \) theo \(AB,BC,CA\).
b) Chứng minh: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\); \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\); \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\); \(\tan \alpha .\cot \alpha = 1\).
Từ đó, tính giá trị biểu thức: \(S = {\sin ^2}35^\circ + {\cos ^2}35^\circ \); \(T = \tan 61^\circ .\cot 61^\circ \).
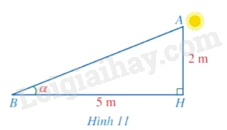
Hình 11 mô tả tia nắng mặt trời dọc theo \(AB\) tạo với phương nằm ngang trên mặt đất một góc \(\alpha = \widehat {ABH}\). Sử dụng máy tính cầm tay, tính số đo góc \(\alpha \) (làm tròn kết quả đến hàng đơn vị của độ), biết \(AH = 2m,BH = 5m\).
Tính tỉ số lượng giác của các góc \(\alpha \) và \(\beta \) trong mỗi trường hợp ở Hình 4.13.

Cho hình chữ nhật ABCD có \(\widehat {ABD} = 2\widehat {CBD}\). Hãy tính tỉ số chiều dài và chiều rộng của hình chữ nhật ABCD.
Khi một vật được ném xiên một góc \(\alpha \) so với mặt đất và tốc độ ném ban đầu là \({v_o}\left( {m/s} \right)\) (Hình 4.14), độ cao lớn nhất H(m) mà vật có thể đạt đến được cho bởi công thức: \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) (nguồn: https://phys.libretexts.org/Bookshelves/University_Physics/Physics_(Boundless)/3%3A_Two-Dimensional_Kinematics/3.3%3A_Projectile_Motion). Tính độ cao lớn nhất của vật nếu tốc độ ném ban đầu là 12m/s và góc ném là:

a) \({45^o}\);
b) \({30^o}\);
c) \({50^o}\).
Làm tròn kết quả đến hàng phần mười mét.
Cho tam giác ABC vuông tại A có \(AC = AB\sqrt 3 \). Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) \(\widehat B = 60^\circ ,\widehat C = 30^\circ \).
b) \(\sin B = \cos B = \frac{{\sqrt 3 }}{2}\).
c) \(\tan B = \cot C = \frac{{\sqrt 3 }}{3}\).
a) Chứng minh rằng với mọi góc nhọn \(\alpha < {45^o}\), ta có
\(\sin \left( {{{45}^o} - \alpha } \right) = \cos \left( {{{45}^o} + \alpha } \right),\cos \left( {{{45}^o} - \alpha } \right) = \sin \left( {{{45}^o} + \alpha } \right)\)
b) Không dùng MTCT, tính
\(\sin {25^o} + \sin {35^o} + \sin {45^o} - \cos {45^o} - \cos {55^o} - \cos {65^o}\)
Với \(\alpha < \beta < {90^o}\), hãy chứng minh rằng:
a) \(\cos \alpha > \cos \beta \) (HD. Sử dụng Ví dụ 5 và bài 4,15);
b) \(\sin \alpha < \sin \beta \) (HD. Sử dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)).
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho tam giác OAB vuông tại O có OA = 8 cm, OB = 15 cm.
a) \(\tan A = \frac{{15}}{8}\)
b) \(\sin B = \frac{{15}}{{17}}\)
c) \(\sin A = \frac{8}{{17}}\)
d) cot A = tan B
Cho tam giác ABC có \(\widehat A = {90^o}\) và \(\widehat C = {30^o}\) như trên Hình 4.3. Tìm khẳng định sai trong các khẳng định sau?
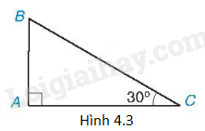
A. \(\sin B = \frac{{\sqrt 3 }}{2}\).
B. \(\cos C = \frac{{\sqrt 3 }}{2}\).
C. \(\tan B = \sqrt 3 \).
D. \(\cot B = \frac{1}{2}\).
Cho tam giác ABC có \(\widehat A = {40^o},\widehat B = {60^o},AB = 6cm\). Hãy tính (làm tròn đến hàng đơn vị):
a) Chiều cao AH và cạnh AC;
b) Độ dài BH và CH.
Một khúc sông rộng khoảng \(100m\) . Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên, nên phải đi khoảng \(180m\) mới sang được bờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một góc bao nhiêu độ? (làm tròn đến độ)
-
A.
\(56^\circ \)
-
B.
\(40^\circ \)
-
C.
\(65^\circ \)
-
D.
\(55^\circ \)







Danh sách bình luận