Xác định tâm sai, tiêu điểm và đường chuẩn tương ứng của mỗi đường conic sau:
a) \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{{12}} = 1\).
b) \(\frac{{{x^2}}}{{14}} - \frac{{{y^2}}}{2} = 1\).
c) \({y^2} = 7x\).
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\).
+ 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right)\).
+ Kích thước của hình chữ nhật cơ sở là 2a và 2b.
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\).
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} \).
+ Độ dài trục lớn: \(2a\), độ dài trục nhỏ: \(2b\).
a) Elip (E): \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{{12}} = 1\) có \(a = 4,b = 2\sqrt 3 \) suy ra \(c = \sqrt {{a^2} - {b^2}} = 2\).
+ Tâm sai: \(e = \frac{c}{a} = \frac{1}{2}\).
+ Tiêu điểm \({F_1}( - 2;0),{F_2}(2;0)\).
+ Đường chuẩn \({\Delta _1}:x + 8 = 0\), \({\Delta _2}:x - 8 = 0\).
b) Hypebol (H) \(\frac{{{x^2}}}{{14}} - \frac{{{y^2}}}{2} = 1\) có \(a = \sqrt {14} ,b = \sqrt 2 \) suy ra \(c = \sqrt {{a^2} + {b^2}} = 4\).
+ Tâm sai: \(e = \frac{c}{a} = \frac{{2\sqrt {14} }}{7}\).
+ Tiêu điểm \({F_1}( - 4;0),{F_2}(4;0)\).
+ Đường chuẩn \({\Delta _1}:x + \frac{7}{2} = 0\), \({\Delta _2}:x - \frac{7}{2} = 0\).
c) Parabol (P) \({y^2} = 7x\) có \(2p = 7\) hay \(p = \frac{7}{2}\).
+ Tâm sai: \(e = 1\).
+ Tiêu điểm: \(F\left( {\frac{7}{4};0} \right)\).
+ Đường chuẩn: \(\Delta :x = - \frac{7}{4}\).

Các bài tập cùng chuyên đề
Hãy cho biết quỹ đạo của từng vật thể trong bảng sau đây là parabol, elip hay hypebol.
|
Tên |
Tâm sai của quỹ đạo |
Ngày phát hiện |
|
Sao chổi Halley |
0,967 |
TCN |
|
Sao chổi Hale-Bopp |
0,995 |
23/07/1995 |
|
Sao chổi Hyakutake |
0,999 |
31/01/1996 |
|
Sao chổi C/1980E1 |
1,058 |
11/02/1980 |
|
Oumuamua |
1,201 |
19/10/2017 |
(Theo nssdc.gsfc.nasa.gov và astronomy.com)
Lập phương trình đường conic biết tâm sai bằng \(\frac{2}{3}\), một tiêu điểm \(F( - 2;0)\) và đường chuẩn tương ứng \(\Delta :x + \frac{9}{2} = 0\).
Viết phương trình các đường chuẩn của các đường conic sau:
a) \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
b) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{4} = 1\).
c) \({y^2} = 8x\).
Cho hai elip \(({E_1}):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) và \(({E_2}):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\).
a) Tìm mối quan hệ giữa hai tâm sai của các elip đó.
b) Chứng minh rằng với mỗi điểm M thuộc elip \(({E_2})\) thì trung điểm N của đoạn thẳng OM thuộc elip \(({E_1})\).
Quỹ đạo chuyển động của sao chổi Halley là một elip, nhận tâm Mặt Trời là một tiêu điểm, có tâm sai bằng 0,967.
a) Giải thích vì sao ta có thể coi bất kì hình vẽ elip nào với tâm sai bằng 0,967 là hình ảnh thu nhỏ của quỹ đạo sao chổi Halley.
b) Biết khoảng cách gần nhất từ sao chổi Halley đến tâm Mặt Trời là khoảng \({88.10^6}\) km, tính khoảng cách xa nhất (theo nssdc.gsfc.nasa.gov).
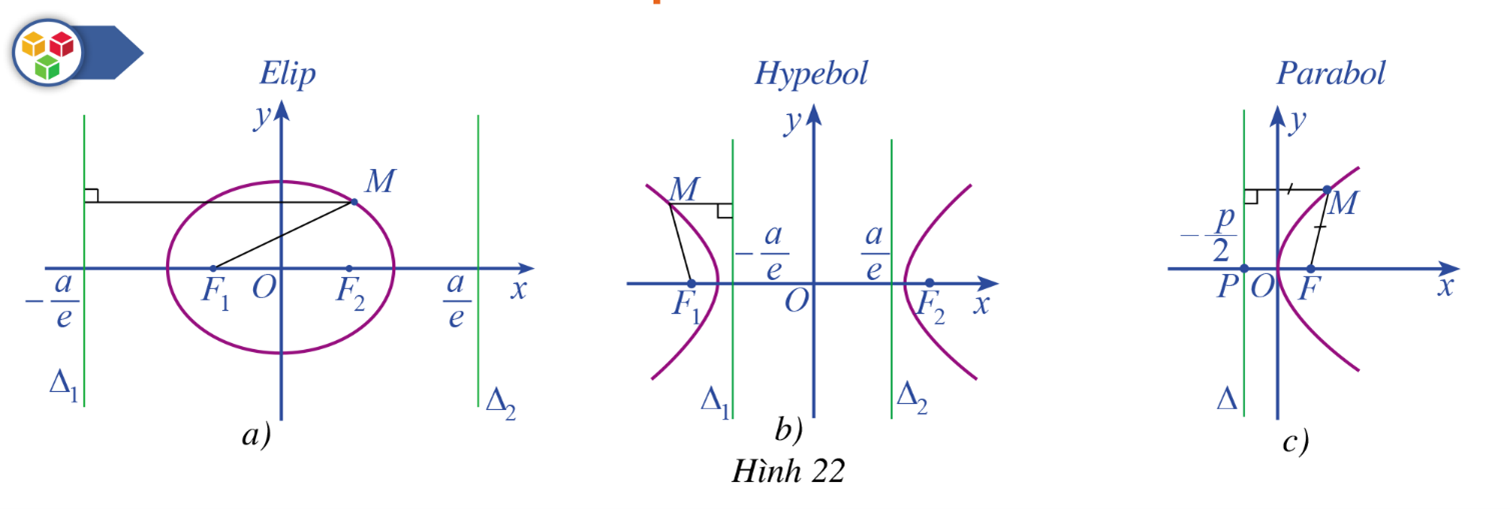
Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.
Cho hình chữ nhật ABCD với bốn đỉnh \(A\left( { - 4;3} \right),B\left( {4;3} \right),C\left( {4; - 3} \right),D\left( { - 4; - 3} \right).\)
a) Viết phương trình chính tắc của elip nhận ABCD là hình chữ nhật cơ sở. Vẽ elip đó.
b) Viết phương trình chính tắc của hypebol nhận ABCD là hình chữ nhật cơ sở. Vẽ hypebol đó.
Các đường conic có phương trình như sau là đường elip hay hypebol? Tìm độ dài các trục, tọa độ tiêu điểm, tiêu cự, tâm sai của các đường conic đó.
a) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\).
b) \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{64}} = 1\).
Cho parabol có phương trình chính tắc \({y^2} = 2x\). Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :x = - 5\) và điểm \(F\left( { - 4;0} \right)\). Lấy 3 điểm \(A\left( { - 3;1} \right),B\left( {2;8} \right),C\left( {0;3} \right)\).
a) Tính các tỉ số sau: \(\frac{{AF}}{{d\left( {A,\Delta } \right)}},\frac{{BF}}{{d\left( {B,\Delta } \right)}},\frac{{CF}}{{d\left( {C,\Delta } \right)}}\).
b) Hỏi mỗi điểm A, B, C lần lượt nằm trên loại đường conic nào nhận F là tiêu điểm và \(\Delta \) là đường chuẩn ứng với tiêu điểm đó?
Vệ tinh nhân tạo lần đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1.342 dặm (1 dặm xấp xỉ 1.609 km). Tìm tâm sai của quỹ đạo đó, biết bán kinh của Trái Đất xấp xỉ 4.000 dặm.
Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có một trong hai tiêu điểm là tâm của Mặt Trời. Biết elip này có bán trục lớn \(a \approx 5,{906.10^6}\left( {km} \right)\) và tâm sai \(e \approx 0,249\) (Nguồn: http://vi.wikimedia.org)
Tìm khoảng cách nhỏ nhất (gần đúng) giữa sao Diêm Dương và Mặt Trời.
Cho đường thẳng \(\Delta \) và điểm O sao cho khoảng cách từ O đến \(\Delta \) là OH = 1 (Hình 39). Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên \(\Delta \). Chứng minh tập hợp các điểm M trong mặt phẳng sao cho \(M{K^2} - M{O^2} = 1\) là một đường parabol.
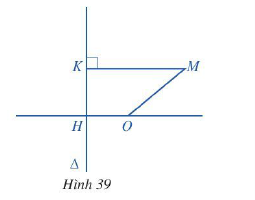
Giao của mặt phẳng và mặt nón trong Hình 2b, c có dạng đường gì?
Gắn một đoạn ống nhựa vào đầu bóng của một đèn chiếu nhỏ để tạo ra một chùm ánh sáng hình mặt nón tròn xoay (Hình 1a, b). Chiếu đèn lên một bức tường với các góp nghiêng khác nhau để ánh sáng từ đèn hắt lên bức tường tạo thành các bóng khác nhau (HÌnh 1c, d, e). Nhận xét hình ảnh bạn nhìn thấy trên bức tường.

Quỹ đạo của các vật thể sau đây là những đường conic. Những đường này là elip, parabol hay hypebol.
|
Tên |
Tâm sai |
|
Trái Đất |
0,0167 |
|
Sao chổi Halley |
0,9671 |
|
Sao chổi Great Southern of 1887 |
1,0 |
|
Vật thể Oumuamua |
1,2 |
(Nguồn: https://vi.wikipedia.org/wiki/oumuamud)
Xác định tâm sai, tọa độ tiêu điểm và phương trình đường chuẩn tương ứng của mỗi đường conic sau:
a) \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{2} = 1\).
b) \(\frac{{{x^2}}}{{12}} - \frac{{{y^2}}}{4} = 1\).
c) \({y^2} = \frac{1}{2}x\).
Cho đường conic có tiêu điểm F, đường chuẩn \(\Delta \) và một điểm M là điểm nằm trên đường conic đó. Tìm mối liên hệ giữa tỉ số \(\frac{{MF}}{{d(M,\Delta )}}\) và tên gọi của đường conic đó.
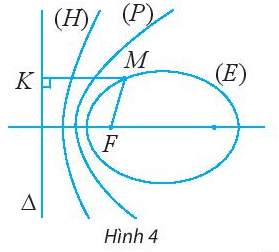
Xác định tâm sai, tọa độ tiêu điểm và phương trình đường chuẩn tương ứng của mỗi đường conic sau:
a) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\).
b) \(\frac{{{x^2}}}{{15}} - \frac{{{y^2}}}{{10}} = 1\).
c) \({y^2} = x\).
Viết phương trình của đường conic có tâm sai bằng 1, tiêu điểm \(F(1;0)\) và đường chuẩn là \(\Delta :x + 1 = 0\).
Viết phương trình của đường conic (C) trong mỗi trường hợp sau:
a) (C) có tiêu điểm \(F(8;0)\), đường chuẩn là \(\Delta :x - 2 = 0\)và tâm sai \(e = 2\).
b) (C) có tiêu điểm \(F( - 4;0)\), đường chuẩn là \(\Delta :x + \frac{{25}}{4} = 0\)và tâm sai \(e = \frac{4}{5}\).
Quỹ đạo của các vật thể sau đây là những đường conic. Những đường này là elip, parabol hay hypebol?
|
Tên |
Tâm sai |
|
Sao Hỏa |
0,0934 |
|
Mặt Trăng |
0,0549 |
|
Sao Thủy |
0,2056 |
|
Sao chổi Ikeya-Seki |
0,9999 |
|
C/2019 Q4 |
3,5 |
(Nguồn: https://vi.wikipedia.org)
Tìm tọa độ các đỉnh, tiêu điểm và bán kính qua tiêu ứng với điểm \(M(x;y)\) của các conic sau:
a) \(\frac{{{x^2}}}{{169}} + \frac{{{y^2}}}{{144}} = 1\).
b) \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{{144}} = 1\).
c) \({y^2} = 11x\).
Cho elip (E): \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\).
a) Xác định tọa độ các đỉnh, tiêu tiêu và tìm tâm sai của (E).
b) Viết phương trình chính tắc của parabol (P) có tiêu điểm có hoành độ dương của (E).
c) Viết phương trình chính tắc của hypebol (H) có hai đỉnh là hai tiêu điểm của (E), hai tiêu điểm là hai đỉnh của (E). Tìm tâm sai của (H).
Cho đường thẳng \(d:x - y + 1 = 0\) và điểm \(F(1;1)\). Viết phương trình của đường conic nhận F là tiêu điểm, d là đường chuẩn và có tâm sai e trong mỗi trường hợp sau:
a) \(e = \frac{1}{2}\).
b) \(e = 1\).
c) \(e = 2\).
Ta đã biết tính chất quang học của ba đường conic (xem phần đọc thêm Bạn có biết? ở trang 72, sách giáo khoa Toán 10, tập hai). Hypebol cũng có tính chất quang học tương tự như elip: Tia sáng hướng tới tiêu điểm \({F_1}\) của hypebol (H) khi gặp một nhánh của (H) sẽ cho tia phản xạ đi qua \({F_2}\).
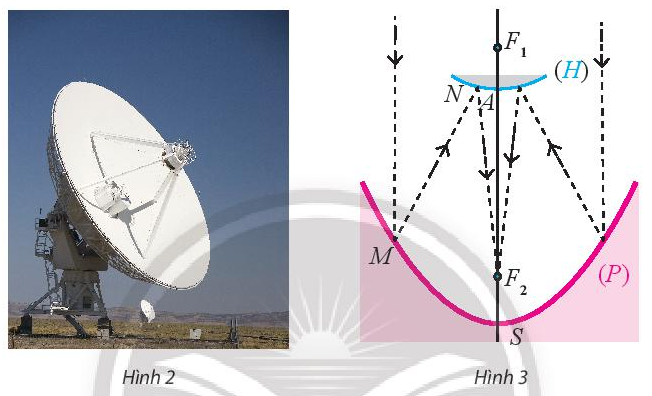
Một nhà nghiên cứu thiết kế một kính thiên văn vô tuyến chứa hai gương có mặt cắt hình parabol (P) và hình một nhánh của hypebol (H). Parabol (P) có tiêu điểm \({F_1}\) và đỉnh S. Hypebol (H) có đỉnh A, có chung một tiều điểm là \({F_1}\) với (P) và còn có tiêu điểm thứ hai \({F_2}\) (Hình 3).
Nguyên tắc hoạt động của kính thiên văn đó như sau: Tin hiệu đến từ vũ trụ được xem như song song với trục của parabol (P), khi đến điểm M của (P) sẽ cho tia phản xa theo hướng \(M{F_1}\) , tia này gặp (H) tại điểm Nvà cho tia phản xạ tới \({F_2}\) là nơi thu tín hiệu. Cho biết \(S{F_1} = 14{\rm{ }}m,{\rm{ }}S{F_2} = 2m\)và \(A{F_1} = 1m\). Hãy viết phương trình chính tắc của (P) và (H).
(Nguồn: https://sciencestruck.com/parabolic-mirror-working-principle-applications)







Danh sách bình luận