Ba lớp 10A, 10B, 10C gồm 128 học sinh cùng tham gia lao động trồng cây. Mỗi học sinh lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. MIỗi học sinh lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi học sinh lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn và 375 cây bàng. Gọi x, y, = lần lượt là số học sinh của các lớp 10A, 10B, 10C.

a) Lập các hệ thức thể hiện mối liên hệ giữa x, y và z.

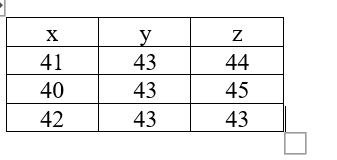
b) Trong bảng dữ liệu sau, chọn các số liệu phủ hợp với số học sinh của mỗi lớp 10A, 10B, 10C và giải thích sự lựa chọn của bạn.

Hệ nào dưới đây là hệ phương trình bậc nhất ba ẩn? Kiểm tra xem bộ ba số (-3; 2; -1) có phải là nghiệm của hệ phương trình bậc nhất ba ẩn đó không.

a) \(\left\{ \begin{array}{l}x + 2y - 3z = 1\\2x - 3y + 7z = 15\\3{x^2} - 4y + z =  - 3\end{array} \right.\)

b) \(\left\{ \begin{array}{l} - x + y + z = 4\\2x + y - 3z =  - 1\\3x\;\;\,\quad  - 2z =  - 7\end{array} \right.\)

Xét hệ phương trình với các ẩn là x, y, z sau:

\(\left\{ \begin{array}{l}x + y + z = 2\\x + 2y + 3z = 1\\2x + y + 3z =  - 1\end{array} \right.\)

a) Mỗi phương trình của hệ trên có bậc mấy đối với các ẩn x, y, z?

b) Thử lại rằng bộ ba số (x; y; z) = (1; 3; -2) thỏa mãn cả ba phương trình của hệ.

c) Bằng cách thay trực tiếp vào hệ, hãy kiểm tra xem bộ ba số (1; 1; 2) có thỏa mãn hệ phương trình đã cho không.

Hà mua văn phòng phẩm cho nhóm bạn cùng lớp gồm Hà, Lan và Minh hết tổng cộng 820 nghìn đồng. Hà quên không lưu hóa đơn của mỗi bạn, nhưng nhớ được rằng số tiền trả cho Lan ít hơn một nửa số tiền trả cho Hà là 5 nghìn đồng, số tiền trả cho Minh nhiều hơn số tiền trả cho Lan là 210 nghìn đồng. Hỏi mỗi bạn Lan và Minh phải trả cho Hà bao nhiêu tiền?

Giải các hệ phương trình sau:

a) \(\left\{ \begin{array}{l}2x + y - 3z = 3\\x + y + 3z = 2\\3x - 2y + z =  - 1\end{array} \right.\)

b) \(\left\{ \begin{array}{l}4x + y + 3z =  - 3\\2x + y - z = 1\\5x + 2y = 1\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x + 2z =  - 2\\2x + y - z = 1\\4x + y + 3z =  - 3\end{array} \right.\)

Cho hệ phương trình \(\left\{ \begin{array}{l}x + y - 2z = 3\\ - x + y + 6z = 13\\2x + y - 9z =  - 5\end{array} \right.\)

a) Khử ẩn x của phương trình thứ hai bằng cách cộng phương trình này với phương trình thứ nhất theo từng vế tương ứng. Viết phương trình nhận được (phương trình này không còn chứa ẩn x và là phương trình thứ hai của hệ mới, tương đương với hệ ban đầu).

b) Khử ẩn x của phương trình thứ ba bằng cách nhân phương trình thứ nhất với -2 rồi cộng với phương trình thứ ba theo từng vế tương ứng. Viết phương trình thứba mới nhận được. Từ đó viết hệ mới nhận được sau hai bước trên (đã khử x ở hai phương trình cuối).

c) Làm tương tự đối với hệ mới nhận được ở câu b), từ phương trình thứ hai và thứ ba khử ẩn y ở phương trình thứ ba. Viết hệ dạng tam giác nhận được.

d) Giải hệ dạng tam giác nhận được ở câu c). Từ đó suy ra nghiệm của hệ đã cho.

Giải hệ phương trình \(\left\{ \begin{array}{l}2x\;\;\quad \,\quad \;\;\, = 3\\\;\,x + \;\;\;y\quad \;\, = 2\\2x - 2y + z =  - 1\end{array} \right.\)

Cho hệ phương trình \(\left\{ \begin{array}{l}x + y - 2z = 3\\\;\,\quad \;\,y + z = 7\\\quad \,\quad \;\;\,2z = 4\end{array} \right.\)

Từ phương trình cuối hãy tính z, sau đó thay vào phương trình thứ hai để tìm y, cuối cùng thay y và z tìm được vào phương trình đầu để tìm x.

Sử dụng máy tính cầm tay tìm nghiệm của các hệ phương trình trong Ví dụ 3, Ví dụ 4, Ví dụ 5 và Luyện tập 3.

Hệ nào dưới đây là hệ phường trình bậc nhất ba ẩn? Kiểm tra xem bộ ba số (2; 0; -1) có phải là nghiệm của hệ phương trình bậc nhất ba ẩn đó không.

a) \(\left\{ \begin{array}{l}x - 2z = 4\\2x + y - z = 5\\ - 3x + 2y =  - 6\end{array} \right.\)

b) \(\left\{ \begin{array}{l}x - 2y + 3z = 7\\2x - {y^2} + z = 2\\x + 2y =  - 1\end{array} \right.\)

Giải các hệ phương trình sau:

a) \(\left\{ \begin{array}{l}2x - y - z = 20\\x + y =  - 5\\x = 10\end{array} \right.\)

b) \(\left\{ \begin{array}{l}x - y - 3z = 20\\x - z = 3\\x + 3z =  - 7\end{array} \right.\)

Giải các hệ phương trình sau bằng phương pháp Gauss.

a) \(\left\{ \begin{array}{l}2x - y - z = 2\\x + y = 3\\x - y + z = 2\end{array} \right.\)

b) \(\left\{ \begin{array}{l}3x - y - z = 2\\x + 2y + z = 5\\ - x + y = 2\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x - 3y - z =  - 6\\2x - y + 2z = 6\\4x - 7y =  - 6\end{array} \right.\)

d) \(\left\{ \begin{array}{l}x - 3y - z =  - 6\\2x - y + 2z = 6\\4x - 7y = 3\end{array} \right.\)

e) \(\left\{ \begin{array}{l}3x - y - 7z = 2\\4x - y + z = 11\\ - 5x - y - 9z =  - 22\end{array} \right.\)

f) \(\left\{ \begin{array}{l}2x - 3y - 4z =  - 2\\5x - y - 2z = 3\\7x - 4y - 6z = 1\end{array} \right.\)

Gọi x, y, z lần lượt là số gà trống, số gà mái, số gà trống cần chuyển sang mục đích nuôi lấy thịt trong đàn gà.

a) Điều kiện của x, y và z là gì?

b) Từ giải thiết của bài toán, hãy tìm ba phương trình bậc nhất ràng buộc x, y và z, từ đó có một hệ phương trình bậc nhất ba ẩn.

c) Giải hệ phương trình bậc nhất thu được. Từ đó đưa ra câu trả lời cho bài toán.

Cho hệ ba phương trình bậc nhất ba ẩn sau:

\(\left\{ \begin{array}{l}{a_1}x + {b_1}y + {c_1}z = {d_1}\\{a_2}x + {b_2}y + {c_2}z = {d_2}\\{a_3}x + {b_3}y + {c_3}z = {d_3}\end{array} \right.\)

a) Giả sử \(({x_0};{y_0};{z_0})\) và \(({x_1};{y_1};{z_1})\) là hai nghiệm phân biệt của hệ phương trình trên.

Chứng minh rằng \(\left( {\frac{{{x_0} + {x_1}}}{2};\frac{{{y_0} + {y_1}}}{2};\frac{{{z_0} + {z_1}}}{2}} \right)\) cũng là một nghiệm của hệ.

b) Sử dụng kết quả của câu a) chứng minh rằng, nếu hệ phương trình bậc nhất ba ẩn có hai nghiệm phân biệt thì nó sẽ có vô số nghiệm.

Giải các hệ phương trình sau:

a) \(\left\{ \begin{array}{l}x + y + z = 6\\x + 2y + 3z = 14\\3x - 2y - z =  - 4\end{array} \right.\)

b) \(\left\{ \begin{array}{l}2x - 2y + z = 6\\3x + 2y + 5z = 7\\7x + 3y - 6z = 1\end{array} \right.\)

c) \(\left\{ \begin{array}{l}2x + y - 6z = 1\\3x + 2y - 5z = 5\\7x + 4y - 17z = 7\end{array} \right.\)

d) \(\left\{ \begin{array}{l}5x + 2y - 7z = 6\\2x + 3y + 2z = 7\\9x + 8y - 3z = 1\end{array} \right.\)

Tìm các số thực A, B và C thỏa mãn:

\(\frac{1}{{{x^3} + 1}} = \frac{A}{{x + 1}} + \frac{{Bx + C}}{{{x^2} - x + 1}}\).

Nếu định nghĩa hai hệ phương trình bậc nhất hai ẩn tương đương.

Cho hệ phương trình  \(\left\{ \begin{array}{l}3x + 2y - 5z =  - 4\\ - x + 3y + 5z = 5\\2x + 7y - 3z = 3\end{array} \right.\) (*)

a) Mỗi phương trình của hệ (*) là phương trình có dạng như thế nào?

b) Bộ số \((x;y;z) = ( - 2;1;0)\) có là nghiệm của từng phương trình trong hệ hay không? Vì sao?

Cho phương trình: \(2x + y - 3z = 1\) (1)

a) Nêu các ẩn của phương trình (1).

b) Với mỗi ẩn của phương trình (1), xác định bậc của ẩn đó.

Giải hệ phương trình:

\(\left\{ \begin{array}{l}x + y - 3z =  - 1\\y - z = 0\\ - x + 2y = 1\end{array} \right.\)

Giải hệ phương trình:

\(\left\{ \begin{array}{l}x + 2y + 6z = 5\\ - x + y - 2z = 3\\x - 4y - 2z = 13\end{array} \right.\)

Giải hệ phương trình:

\(\left\{ \begin{array}{l}4x + y - 3z = 11\\2x - 3y + 2z = 9\\x + y + z =  - 3\end{array} \right.\)

Sử dụng máy tính cầm tay để tìm nghiệm của các hệ phương trình:

\(\left\{ \begin{array}{l}2x - 3y + 4z =  - 5\\ - 4z + 5y - z = 6\\3x + 4y - 3z = 7\end{array} \right.\)

Kiểm tra xem mỗi bộ số \((x;y;z)\) đã cho có là nghiệm của hệ phương trình tương ứng hay không?

a) \(\left\{ \begin{array}{l}x + 3y + 2z = 1\\5x - y + 3z = 16\\ - 3x + 7y + z =  - 14\end{array} \right.\) \((0;3; - 2),(12;5; - 13),(1; - 2;3)\)

b) \(\left\{ \begin{array}{l}3x - y + 4z =  - 10\\ - x + y + 2z = 6\\2x - y + z =  - 8\end{array} \right.\) \(\left( { - 2;4;0} \right),\left( {0; - 3;10} \right),\left( {1; - 1;5} \right)\)

c) \(\left\{ \begin{array}{l}x + y + z = 100\\5x + 3y + \frac{1}{3}z = 100\end{array} \right.\) \(\left( {4;18;78} \right),\left( {8;11;81} \right),\left( {12;4;84} \right)\)

Giải hệ phương trình:

a) \(\left\{ \begin{array}{l}x - 2y + 4z = 4\\3y - z = 2\\2z =  - 10\end{array} \right.\)

b) \(\left\{ \begin{array}{l}4x + 3y - 5z =  - 7\\2y = 4\\y + z = 3\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x + y + 2z = 0\\3x + 2y = 2\\x = 10\end{array} \right.\)

Giải hệ phương trình:

a) \(\left\{ \begin{array}{l}3x - y - 2z = 5\\2x + y + 3z = 6\\6x - y - 4z = 9\end{array} \right.\)

b) \(\left\{ \begin{array}{l}2x + y - 3z = 5\\3x - y + z = 4\\7x + y - 5z =  - 2\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x + 2y - 4z =  - 1\\2x - y - 3z = 3\\x - 3y + z = 4\end{array} \right.\)

Sử dụng máy tính cầm tay để tìm nghiệm của các hệ phương trình:

a) \(\left\{ \begin{array}{l} - x + 2y - 3z = 2\\2x + y + 2z =  - 3\\ - 2x - 3y + z = 5\end{array} \right.\)

b) \(\left\{ \begin{array}{l}x - 3y + z = 1\\5y - 4z = 0\\x + 2y - 3z =  - 1\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x + y - 3z =  - 1\\3x - 5y - z =  - 3\\ - x + 4y - 2z = 1\end{array} \right.\)

Tổng số hạt p, n, e trong hai nguyên tử kim loại A và B là 177. Trong đó số hạt mang điện nhiều hơn số hạt không mang điện là 47. Số hạt mang điện của nguyên tử B nhiều hơn của nguyên tử A là 8. Xác định số hạt proton trong một nguyên tử A.

Hệ nào dưới đây là hệ phương trình bậc nhất ba ẩn? Mỗi bộ ba số (1; 5; 2), (1;1;1) và (-1; 2; 3) có là nghiệm của hệ phương trình bậc nhất ba ẩn đó không?

(1) \(\left\{ \begin{array}{l}4x - 2y + z = 5\\4xz - 5y + 2z =  - 7\\ - x + 3y + 2z = 3\end{array} \right.\)

(2) \(\left\{ \begin{array}{l}x + 2z = 5\\2x - y + z =  - 1\\3x\; - 2y =  - 7\end{array} \right.\)

Sử dụng máy tính cầm tay, tìm nghiệm của các hệ phương trình sau:

a) \(\left\{ \begin{array}{l}2x + y - z =  - 1\\x + 3y + 2z = 2\\3x + 3y - 3z =  - 5\end{array} \right.\)

b) \(\left\{ \begin{array}{l}2x - 3y + 2z = 5\\x + 2y - 3z = 4\\3x - y - z = 2\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x - y - z =  - 1\\2x - y + z =  - 1\\ - 4x + 3y + z = 3\end{array} \right.\)

Trong các hệ phương trình sau, hệ nào là hệ phường trình bậc nhất ba ẩn? Mỗi bộ ba số (-1;2;1), (-1,5; 0,25; -1,25) có là nghiệm của hệ phương trình bậc nhất ba ẩn đó không?

a) \(\left\{ \begin{array}{l}3x - 2y + z =  - 6\\ - 2x + y + 3z = 7\\4x - y + 7z = 1\end{array} \right.\)

b) \(\left\{ \begin{array}{l}5x - 2y + 3z = 4\\3x + 2yz - z = 2\\x - 3y + 2z =  - 1\end{array} \right.\)

c) \(\left\{ \begin{array}{l}2x - 4y - 3z = \frac{{ - 1}}{4}\\3x + 8y - 4z = \frac{5}{2}\\2x + 3y - 2z = \frac{1}{4}\end{array} \right.\)