Một con ngựa giá 204 đồng (đơn vị tiền cổ). Có ba người muốn mua nhung mỗi người không đủ tiển mua. Người thứ nhất nói với hai người kia: “Mỗi anh cho tôi vay một nửa số tiền của mình thì tôi đủ tiền mua ngựa"; Người thứ hai nói: "Mỗi anh cho tôi vay một phần ba số tiền của mỉnh, tôi sẽ mua được ngựa"; Người thú ba lại nói: "Chỉ cần mỗi anh cho tôi vay một phần tư số tiền của mình thi con ngựa sẽ là của tôi". Hỏi mỗi người có bao nhiêu tiển?
Bước 1: Lập hệ phương trình.
+ Chọn ẩn và đặt điều kiện cho ẩn.
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết.
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải hệ phương trình.
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Gọi số tiền mỗi người có lần lượt là x, y, z (đồng) (\(x,y,z \ge 0\)).
Người thứ nhất nói với hai người kia: “Mỗi anh cho tôi vay một nửa số tiền của mình thì tôi đủ tiền mua ngựa" tức là: \(x + \frac{1}{2}y + \frac{1}{2}z = 204\).
Người thứ hai nói: "Mỗi anh cho tôi vay một phần ba số tiền của mỉnh, tôi sẽ mua được ngựa" tức là: \(\frac{1}{3}x + y + \frac{1}{3}z = 204\).
Người thứ ba lại nói: "Chỉ cần mỗi anh cho tôi vay một phần tư số tiền của mình thi con ngựa sẽ là của tôi" tức là: \(\frac{1}{4}x + \frac{1}{4}y + z = 204\).
Từ đó ta có hệ phương trình bậc nhất ba ẩn \(\left\{ \begin{array}{l}x + \frac{1}{2}y + \frac{1}{2}z = 204\\\frac{1}{3}x + y + \frac{1}{3}z = 204\\\frac{1}{4}x + \frac{1}{4}y + z = 204\end{array} \right.\)
Dùng máy tính cầm tay, giải hpt ta được \(x = 60,y = 132,z = 156\).
Vậy người thứ nhất có 60 đồng, người thứ hai có 132 đồng và người thứ ba có 156 đồng.

Các bài tập cùng chuyên đề
Tại một quốc gia, khoảng 400 loài động vật nằm trong danh sách các loài có nguy cơ tuyệt chủng. Các nhóm động vật có vú, chim và cá chiếm 55% các loài có nguy cơ tuyệt chủng. Nhóm chim chiếm nhiều hơn 0,7% so với nhóm cá, nhóm cá chiếm nhiều hơn 1,5% so với đồng vật có vú. Hỏi mỗi nhóm động vật có vú, chim và cá chiếm bao nhiêu phần trăm trong các loài có nguy cơ tuyệt chủng?
Cân bằng phản ứng hóa học đốt cháy octane trong oxygen.
\({C_{18}}{H_{18}} + {O_2} \to C{O_2} + {H_2}O\)
Cho hàm cung và hàm cầu của ba mặt hàng như sau:
\(\begin{array}{l}{Q_{{S_1}}} = - 4 + x;{Q_{{D_1}}} = 70 - x - 2y - 6z;\\{Q_{{S_2}}} = - 3 + y;{Q_{{D_2}}} = 76 - 3x - y - 4z;\\{Q_{{S_3}}} = - 6 + 3z;{Q_{{D_3}}} = 70 - 2x - 3y - 2z.\end{array}\)
Hãy xác định giá cân bằng cung – cầu của ba mặt hàng.
Ba người cùng làm việc cho một công ty với vị trí lần lượt là quản lí kho, quản lí văn phòng và tài xế xe tải. Tổng tiền lương hằng năm của người quản lí kho và người quản lí văn phòng là 164 triệu đồng, còn của người quản lí kho và tài xế xe tải là 156 triệu đồng. Mỗi năm, người quản lí kho lĩnh lương nhiều hơn tài xế xe tải 8 triệu đồng. Hỏi lương hằng năm của mỗi người là bao nhiêu?
Năm ngoái, người ta có thể mua ba mẫu xe ô tô của ba hãng X, Y, Z với tổng số tiền là 2,8 tỉ đồng. Năm nay, do lạm phát, để mua chiếc xe đó cần 3,018 tỉ đồng. Giá xe ô tô của hãng X tăng 8%, của hãng Y tăng 5% và của hãng Z tăng 12%. Nếu trong năm ngoái giá của chiếc xe của hãng Y thấp hơn 200 triệu đồng so với giá chiếc xe của hãng X thì giá của mỗi chiếc xe trong năm ngoái là bao nhiêu?
Cân bằng phản ứng hóa học đốt cháy octane trong oxygen:
\({C_{18}}{H_{18}} + {O_2} \to C{O_2} + {H_2}O\).
Gọi x, y, z lần lượt là số gà trống, số gà mái, số gà trống cần chuyển sang mục đích nuôi lấy thịt trong đàn gà.
a) Điều kiện của x, y và z là gì?
b) Từ giải thiết của bài toán, hãy tìm ba phương trình bậc nhất ràng buộc x, y và z, từ đó có một hệ phương trình bậc nhất ba ẩn.
c) Giải hệ phương trình bậc nhất thu được. Từ đó đưa ra câu trả lời cho bài toán.
Xét thị trường hải sản gồm ba mặt hàng là cua, tôm và cá. Kí hiệu x, y, z lần lượt là giá 1 kg cua, 1kg tôm và 1kg cá (đơn vị nghìn đồng). Kí hiệu \({Q_{{S_1}}}\), \({Q_{{S_2}}}\) và \({Q_{{S_3}}}\) là lượng cua, tôm và cá mà người bán bằng lòng bán với giá x, y và z. Kí hiệu \({Q_{{D_1}}}\), \({Q_{{D_2}}}\) và \({Q_{{D_3}}}\) tương ứng là lượng cua, tôm và cá mà người mua bằng lòng mua với giá x, y và z. Cụ thể các hàm này được cho bởi:
\(\begin{array}{l}{Q_{{S_1}}} = - 300 + x;{Q_{{D_1}}} = 1300 - 3x + 4y - z;\\{Q_{{S_2}}} = - 450 + 3y;{Q_{{D_2}}} = 1150 + 2x - 5y - z;\\{Q_{{S_3}}} = - 400 + 2z;{Q_{{D_3}}} = 900 - 2x - 3y + 4z.\end{array}\)
Tìm mức giá cua, tôm và cá mà người bán và người mua cùng hài lòng.
Em Hà so sánh tuổi của mình với chị Mai và anh Nam. Tuổi của anh Nam gấp ba lần tuổi của em Hà. Cách đây bảy năm tuổi của chị Mai bằng nửa số tuổi của anh Nam. Ba năm nữa tuổi của anh Nam bằng tổng số tuổi của chị Mai và em Hà. Hỏi tuổi của mỗi người là bao nhiêu?
Bác Việt có 330 740 nghỉn đồng, bác chia số tiền này thành ba phần và đem đầu tư vào ba hình thức: Phần thứ nhất bác đầu tư vào chứng khoán với lãi thu được 4% một năm; phần thứ hai bác mua vàng thu lãi 5% một năm và phần thứ ba bác gửi tiết kiệm với lãi suất 6% một năm. Sau một năm, kể cả gốc và lãi bác thu được ba món tiền bằng nhau. Hỏi tổng số tiền cả gốc và lãi bác thu được sau một năm là bao nhiêu?
Một tuyến cáp treo có ba loại vé sau đây: vé đi lên giá 250 nghìn đồng, vé đi xuống giá 200 nghìn đồng và vé hai chiều giá 400 nghìn đồng. Một ngày nhà ga cáp treo thu được tổng số tiền là 251 triệu đồng. Tìm số vé bán ra mỗi loại, biết rằng nhân viên quản lí cáp treo đếm được 680 lượt người đi lên và 520 lượt người đi xuống.
Ba lớp 10A, 10B, 10C của một trường trung học phổ thông gồm 128 em cùng tham gia lao động trồng cây. Tính trung bình, mỗi em lớp 10A trổng được 3 cây xoan và 4 cây bạch đàn; mỗi em lớp 10B trồng được 2 cây xoan và 5 cây bạch đàn; mỗi em lớp 10C trồng được 6 cây xoan. Cả ba lớp trồng được tổng cộng 476 cây xoan và 375 cây bạch đàn. Hỏi mỗi lớp có bao nhiêu em?
Cân bằng phương trình phản ứng hóa học đốt cháy methane trong oxygen:
\(C{H_4} + {O_2} \to C{O_2} + {H_2}O\).
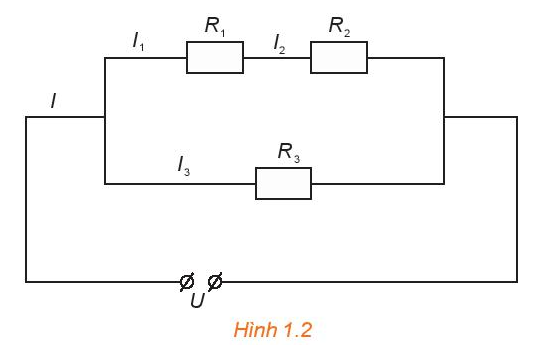
Cho đoạn mạch như Hình 1.2. Gọi I là cường độ dòng điện của mạch chính, \({I_1},{I_2}\)và \({I_3}\) là cường độ dòng điện mạch rẽ. Cho biết \({R_1} = 6\Omega ,{\rm{ }}{R_2} = 8\Omega ,I = 3A\)và \({I_3} = 2A\). Tính điện trở \({R_3}\) và hiệu điện thế U giữa hai đầu đoạn mạch.
Mỗi giai đoạn phát triển của thực vật cần phân bón với tỉ lệ N, P, K nhất định. Bác An làm vườn muốn bón phân cho một cây cảnh có tỉ lệ N :P : K cân bằng nhau. Bác An có ba bao phân bón:
Bao 1 có tỉ lê N : P : K là 12 : 7 : 12.
Bao 2 có tỉ lê N : P : K là 6 : 30 : 25.
Bao 3 có tỉ lệ N : P : K là 30 : 16 : 11.
Hỏi phải trộn ba loại phân bón trên với tỉ lệ bao nhiêu để có hỗn hợp phân bón với tỉ lệ N : P : K là 15:15:15?
Chú ý rằng trên mỗi bao phân người ta thường viết một tỉ lệ N : P : K nhất định. Chẳng hạn trên bao phân 1 ghi tỉ lệ N : P : K là 12 : 7 : 12 nghĩa là hàm lượng đạm N (nitơ) chiếm12%, lân P (tức là P2Os) chiếm 7% và kali K (tức là K,O) chiếm 12%, còn các loại khác chiếm 100%-(12% +7% +12%) = 69%.
Tìm parabol \(y = a{x^2} + bx + c\) trong mỗi trường hợp sau:
a) Parabol đi qua ba điểm A(2;-1), B(4;3) và C(-1;8);
b) Parabol nhận đường thẳng \(x = \frac{5}{2}\) làm trục đối xứng và đi qua hai điểm M(1;0), N(5;-4).
Trong mặt phẳng tọa độ, viết phương trình đường tròn đi qua ba điểm A(0;1), B(2;3) và C(4;1).
Một đoàn xe chở 255 tấn gạo tiếp tế cho đồng bào vùng bị lũ lụt. Đoàn xe có 36 chiếc gồm ba loại: xe chở 5 tấn, xe chở 7 tấn và xe chở 10 tấn. Biết rằng tổng số hai loại xe chở 5 tấn và chở 7 tấn nhiều gấp ba lần số xe chở 10 tấn. Hỏi mỗi loại xe có bao nhiêu chiếc?
Bác An là chủ cửa hàng kinh doanh cà phê cho những người sành cà phê. Bác có ba loại cà phê nổi tiếng của Việt Nam: Aribica, Robusta và Moka với giá bán lần lượt là 320 nghìn đồng/kg, 280 nghìn đồng/kg và 260 nghìn đồng/kg. Bác muốn trộn ba loại cà phê này để được một hỗn hợp cà phê, sau đó đóng thành các gói 1kg, bán với giá 300 nghìn đồng/kg và lượng cà phê Moka gấp đôi lượng cà phê Robusta trong mỗi gói. Hỏi bác cần trộn ba loại cà phê này theo tỉ lệ nào?
Bác Việt có 12 ha đất canh tác để trồng ba loại cây: ngô, khoai tây và đậu tương. Chi phí trồng 1 ha ngô là 4 triệu đồng, 1 ha khoai tây là 3 triệu đồng và 1 ha đậu tương là 4,5 triệu đồng. Do nhu cầu thị trường, bác đã trồng khoai tây trên phần diện tích gấp đôi diện tích trồng ngô. Tổng chi phí trồng ba loại cây trên là 45,25 triệu đồng. Hỏi diện tích trồng mỗi loại cây là bao nhiêu?
Cân bằng phương trình phản ứng hóa học sau:
\(Fe{S_2} + {O_2} \to F{e_2}{O_3} + S{O_2}\).
Bạn Mai có ba lọ dung dịch chứa một loại acid. Dung dịch A chứa 10%, dung dịch B chứa 30% và dung dịch C chứa 50% acid. Bạn Mai lấy từ mỗi lọ một lượng dung dịch và hòa với nhau để có 50g hỗn hợp chứa 32% acid này và lượng dung dịch loại C lấy nhiều gấp đôi dung dịch loại A. Tính lượng dung dịch mỗi loại bạn Mai đã lấy.
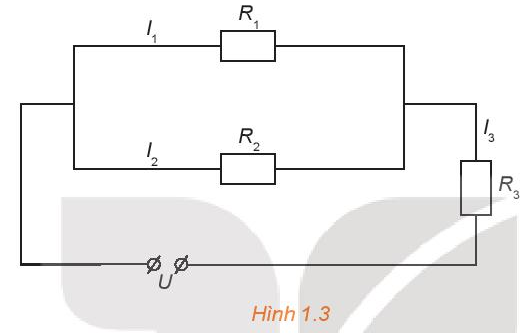
Cho đoạn mạch như Hình 1.3. Biết \({R_1} = 36\Omega ,{\rm{ }}{R_2} = 45\Omega ,{I_3} = 1,5A\) là cường độ dòng điện trong mạch chính và hiệu điện thế giữa hai đầu đoạn mạch U = 60V. Gọi \({I_1}\) và \({I_2}\) là cường độ dòng diện trong mạch rẽ. Tính \({I_1},{I_2}\)và \({R_3}.\)
Giải bài toán dân gian sau:
Em đi chợ phiên
Anh gửi một tiền
Cam, thanh yên, quýt
Không nhiều thỉ ít
Mua đủ một trǎm
Cam ba đồng một
Quýt một đồng năm
Thanh yên tươi tôt
Năm đồng một trái.
Hỏi mỗi thứ mua bao nhiêu trái, biết một tiển bằng 60 đồng?
Tìm số đo ba góc của một tam giác, biết tổng số đo của góc thứ nhất và góc thứ hai bằng hai lần số đo của góc thứ ba, số đo của góc thứ nhất lớn hơn số đo của góc thứ ba là \({20^o}\).
Bác Thanh chia số tiền 1 tỉ đồng của mình cho ba khoản đầu tư. Sau một năm, tổng số tiền lãi thu được là 84 triệu động. Lãi suất cho ba khoản đầu tư lần lượt là 6%, 8%, 15% và số tiền đầu tư cho khoản thứ nhất bằng tổng số tiền đầu tư cho khoản thứ hai và thứ ba. Tính số tiền bác Thanh đầu tư cho mỗi khoản.
Khi một quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống. Biết quỹ đạo chuyển động quả quả bóng là một parabol và độ cao h của quả bóng được tính bởi công thức \(h = \frac{1}{2}a{t^2} + {v_0}t + {h_0}\), trong đó độ cao h và độ cao ban đầu \({h_0}\) được tính bằng mét, t là thời gian của chuyển động tính bằng \(m/{s^2}\), \({v_0}\) là vận tốc ban đầu được tính bằng \(m/s\). Tìm \(a,{v_0},{h_0}\) biết sau 0,5 giây quả bóng đạt được độ cao \(6,075m\); sau 1 giây quả bóng đạt được độ cao \(8,5m\); sau 2 giây quả bóng đạt được độ cao \(6m\).
Một cửa hàng bán đồ nam gồm áo sơ mi, quần âu và áo phông. Ngày thứ nhất bán được 22 áo sơ mi, 12 quần âu và 18 áo phông, doanh thu là 12 580 000 đồng. Ngày thứ hai bán được 16 áo sơ mi, 10 quần âu và 20 áo phông, doanh thu là 10 800 000 đồng. Ngày thứ ba bán được 24 áo sơ mi, 15 quần âu và 12 áo phông, doanh thu là 12 960 000 đồng. Hỏi giá bán mỗi áo sơ mi, mỗi quần âu và mỗi áo phông là bao nhiêu? Biết giá từng loại trong ba ngày không thay đổi.
Ba nhãn hiệu bánh quy là A, B, C được ung cấp bởi một nhà phân phối. Với tỉ lệ thành phần dinh dưỡng theo khối lượng, bánh quy nhãn hiệu A chứa 20% protein, bánh quy nhãn hiệu B chứa 28% protein và bánh quy nhãn hiệu C chứa 30% protein. Một khách hàng muốn mua một đơn hàng như sau:
Mua tổng cộng 224 cái bánh quy bao gồm cả ba nhãn hiệu A, B, C.
Lượng protein trung bình của đơn hàng này (gồm cả ba nhãn hiệu A, B, C) là 25%.
Lượng bánh quy nhãn hiệu A gấp đôi lượng bánh quy nhãn hiệu C.
Tính lượng bánh quy mỗi loại mà khách hàng đó đặt mua.
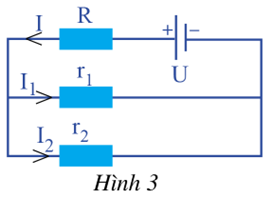
Cho mạch điện như Hình 3. Biết \(U = 20V,R = 0,5\Omega ,\;{r_1} = 1\Omega ,{r_2} = 2\Omega\). Tìm cường độ dòng điện \({I_1},{I_2},I\) chạy qua mỗi điện trở.







Danh sách bình luận