Trong Hình 40, hình màu xanh là ảnh của hình màu cam qua một phép quay. Xác định tâm và góc quay của phép quay đó.

Xác định tâm và góc quay dựa vào định nghĩa:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
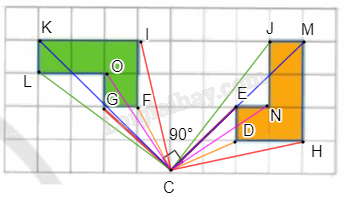
Ta thấy:
+)\(CH{\rm{ }} = {\rm{ }}CI,{\rm{ }}CM{\rm{ }} = {\rm{ }}CK,{\rm{ }}CJ{\rm{ }} = {\rm{ }}CL,{\rm{ }}CN{\rm{ }} = {\rm{ }}CO,{\rm{ }}CE{\rm{ }} = {\rm{ }}CG,{\rm{ }}CD{\rm{ }} = {\rm{ }}CF\;\) (đường chéo của các hình chữ nhật có cùng kích thước).
+) \(\widehat {HCI} = \widehat {MCK} = \widehat {JCL} = \widehat {NCO} = \widehat {ECG} = \widehat {DCF} = 90^\circ \).
Do đó, ta có phép quay tâm C, góc quay 90° biến các điểm H, M, J, N, E, D tương ứng thành các điểm I, K, L, O, G, F.
Như vậy, hình màu xanh là ảnh của hình màu cam quay phép quay tâm C, góc quay 90°.

Các bài tập cùng chuyên đề
Bàn ăn tròn đông người thường được thiết kế sao cho mặt trong nơi đặt đồ ăn có thể quay quanh tâm của nó. Nhờ đó, đồ ăn trên bàn có thể đi tới được gần từng người, mà vị trí đặt mặt bàn không bị dịch chuyển. Cơ sở toán học nào cho phép thực hiện điều đó?

Trong Hình 1.22, tam giác ABC đều.
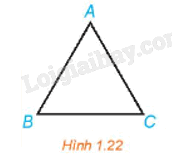
Hãy chỉ ra ảnh của điểm B qua phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\).
Gọi D là ảnh của C qua phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\).
Hỏi B và D có mối quan hệ gì đối với đường thẳng AC?
Phép quay với góc quay bằng 0 có gì đặc biệt?
Ở mặt bàn ăn quay nói trên, trong một lần quay, nếu một đĩa thức ăn trên bàn được quay một phần tư vòng tới vị trí người mới, thì mỗi đĩa không đặt ở chính giữa bàn có được quay một phần tư vòng tới vị trí mới hay không?
Trong tình huống mở đầu, mặt bàn tròn đặt đồ ăn được thiết kế để có thể quay quanh tâm mặt bàn. Coi mặt bàn tròn là hình tròn tâm O, bán kính R. Hỏi, khi thực hiện phép quay tâm O với góc quay \(\alpha \) bất kì thì:
- Điểm O biến thành điểm nào?
- Đường tròn (O, R) biến thành đường tròn nào?
- Vị trí của mặt bàn có bị dịch chuyển hay không?
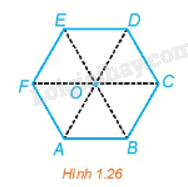
Trong Hình 1.26, ABCDEF là lục giác đều có tâm O. Tìm ảnh của tam giác ACE qua các phép quay \({Q_{\left( {O,\,\frac{\pi }{3}} \right)}},\,\,{Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\)
Khi mặt bàn ăn quay, mặc dù các đĩa thức ăn trên bàn đều dịch chuyển tới vị trí mới nhưng khoảng cách giữa hai đĩa thức ăn có bị thay đổi hay không?
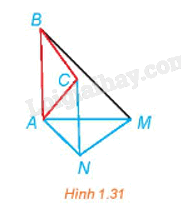
Trong Hình 1.31, BAM và CAN là các tam giác vuông cân tại A. Hãy chỉ ra một phép quay biến tam giác ABC thành tam giác AMN.
Cho hình vuông ABCD có tâm O. Trên đường tròn ngoại tiếp hình vuông, theo chiều dương (ngược chiều kim đồng hồ), thứ tự các đỉnh hình vuông là A, B, C, D.
a) Tìm ảnh của các điểm A, B, C, D qua phép quay tâm O góc quay \(\;\frac{\pi }{2}\).
b) Mỗi phép quay \({Q_{(O,{\rm{ }}o)}},\)\({Q_{\left( {O,\,\frac{\pi }{2}} \right)}},\,{Q_{\left( {O,\,\pi } \right)}},\,{Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến hình vuông ABCD thành hình nào?
Cho hình bình hành ABCD với tâm O.
a) Tìm ảnh của đường thẳng AB qua phép đối xứng tâm O.
b) Tìm ảnh của tam giác ABC qua phép đối xứng tâm O.
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{y^2}\; = {\rm{ }}1.\)
a) Tìm tọa độ tâm đường tròn (C') là ảnh của đường tròn (C) qua \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\).
b) Viết phương trình (C').
Bằng quan sát Hình 1.32, hãy chỉ ra một cách cắt hình đó thành ba phần giống nhau.

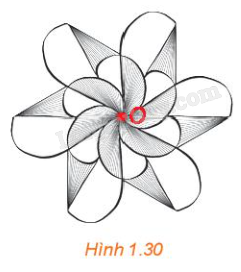
Quan sát Hình 1.30, những phát biểu nào trong các phát biểu sau là đúng?
a) Hình vẽ nhận điểm O (được tô đỏ) làm tâm đối xứng.
b) Một đường thẳng bất kì đi qua điểm O sẽ chia hình vẽ thành hai nửa A và B giống nhau. Nếu thực hiện phép quay tâm O, góc quay 180∘ thì nửa A biến thành nửa B, tức là, B là ảnh của A qua một phép đối xứng tâm O.
c) Có thể chia hình vẽ thành bốn phần giống nhau.
Cho hình hình hành ABCD có hai đường chéo cắt nhau tại O. Tìm ảnh của đường thẳng AB qua \(Đ_{O}\).
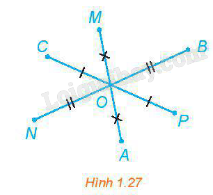
Trong hình 1.27, hãy chỉ ra ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0. Viết phương trình của đường tròn (C') là ảnh của đường tròn (C) qua phép đối xứng tâm A(3; – 3).
Trong mặt phẳng, cho hình tròn tâm O, kí hiệu là ℋ (Hình 22). Xét phép đối xứng tâm ĐO. Tìm ℋ' = ĐO(ℋ).

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1).
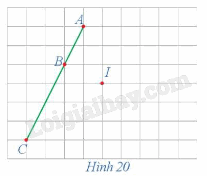
Xét phép đối xứng tâm I (Hình 20).
a) Xác định các điểm A', B', C' là ảnh của ba điểm thẳng hàng A, B, C qua phép đối xứng tâm I.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng tâm O.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
Cho bát giác đều ABCDEGHK với tâm I. Xác định ảnh của các điểm A, B, C, D qua phép đối xứng tâm I.
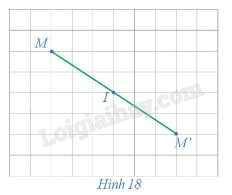
Trong mặt phẳng cho điểm I. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I) (Hình 18).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3) bán kính R = 2. Xác định ảnh của (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90°.
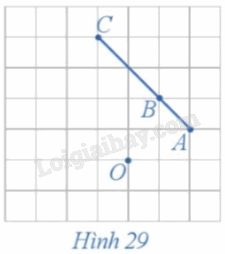
Xét phép quay tâm O với góc quay 90° (Hình 29).
a) Xác định các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
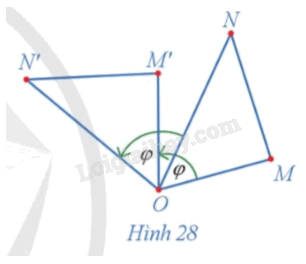
Trong Hình 28, cho các điểm M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ.
a) Hai tam giác OM'N' và OMN có bằng nhau hay không?
b) So sánh hai đoạn thẳng M'N' và MN.
Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°.
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).

Phép đối xứng tâm có là phép quay hay không? Vì sao?
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
a) Trung điểm các cạnh AB, BC, CD, DA;
b) Các đường thẳng AB, AC.
Hình 44 mô tả một viên gạch trang trí hình tam giác đều. Xác định phép quay biến:
a) Cánh hoa màu xanh đỉnh A thành cánh hoa màu xanh đỉnh B.
b) Cánh hoa màu đỏ đỉnh E thành cánh hoa màu đỏ đỉnh D.







