Trong mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm M(x; y) thành điểm M'(3x; – 3y).
a) Tìm ảnh của các điểm O(0; 0), N(2; 1).
b) Chứng minh rằng f là một phép đồng dạng. Tìm tỉ số đồng dạng.
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\).
a) Ảnh của điểm O(0; 0) qua phép biến hình f là \(O'\left( {3{\rm{ }}.{\rm{ }}0;{\rm{ }}-{\rm{ }}3{\rm{ }}.{\rm{ }}0} \right){\rm{ }} \equiv {\rm{ }}O\left( {0;{\rm{ }}0} \right).\)
Ảnh của điểm N(2; 1) qua phép biến hình f là N'(3 . 2; – 3 . 1) = N'(6; – 3).
b) Chọn hai điểm \(M\left( {x;{\rm{ }}y} \right),{\rm{ }}N\left( {z;{\rm{ }}t} \right)\) bất kì. Gọi M', N' tương ứng là ảnh của M, N qua phép biến hình f. Khi đó \(M'\left( {3x;{\rm{ }}-{\rm{ }}3y} \right),{\rm{ }}N'\left( {3z;{\rm{ }}-{\rm{ }}3t} \right).\)
Ta có: \(MN{\rm{ }} = \sqrt {{{\left( {z - x} \right)}^2} + {{\left( {t - y} \right)}^2}} \).
\(M'N' = \sqrt {{{\left( {3z - 3x} \right)}^2} + {{\left( { - 3t - \left( { - 3y} \right)} \right)}^2}} = \sqrt {9{{\left( {z - x} \right)}^2} + 9{{\left( {t - y} \right)}^2}} = 3\sqrt {{{(z - x)}^2} + {{(t - y)}^2}} \).
Suy ra M'N' = 3MN.
Vậy phép biến hình f là phép đồng dạng với tỉ số k = 3.

Các bài tập cùng chuyên đề
Phép dời hình cho phép ta thể hiện mối quan hệ giống nhau cả về hình dạng và kích thước giữa các hình. Đối với các hình chỉ giống nhau về hình dạng còn kích thước có thể khác nhau thì sao? Đối tượng toán học nào cho phép ta thể hiện điều đó?

Trong hai hình Dinh Thống Nhất ở Hình 1.50, hãy chỉ ra phép đồng dạng biến hình nhỏ thành hình lớn.

Cho đường thẳng d và hai điểm phân biệt A, B. Điểm M thay đổi trên đường thẳng d. Gọi N là điểm đối xứng của M qua đường thẳng AB và P là trung điểm của đoạn thẳng BN. Chứng minh rằng P thuộc một đường thẳng cố định.
Chứng minh rằng phép biến hình có được bằng cách thực hiện liên tiếp phép đồng dạng f với tỉ số k1 và phép đồng dạng g với tỉ số k2 là một phép đồng dạng với tỉ số k1.k2.
Phép dời hình và phép vị tự tỉ số t có phải là các phép đồng dạng hay không? Nếu có thì tỉ số đồng dạng là bao nhiêu?
Hai tấm ảnh Dinh Thống Nhất ở hình trên giống nhau về hình dạng, chỉ khác nhau về kích thước.
a) Hãy đo và cho biết chiều dài, chiều rộng của tấm ảnh lớn tương ứng gấp mấy lần chiều dài, chiều rộng của tấm ảnh nhỏ.
b) Nếu lấy hai vị trí A, B bất kì thuộc tấm ảnh nhỏ và các vị trí A', B' tương ứng với chúng trên tấm ảnh lớn thì khoảng cách giữa A' và B' gấp mấy lần khoảng cách giữa A và B? Hãy lấy ví dụ cụ thể các vị trí và đo để kiểm tra câu trả lời của bạn.
Một phép đồng dạng biến ba đỉnh A, B, C của tam giác ABC tương ứng thành A', B', C'. Chứng minh rằng \(\frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}} = \frac{{AB}}{{A'B'}}\).
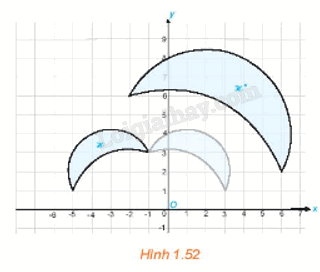
Hai hình ℋ và ℋ " trong Hình 1.52 được vẽ trên mặt phẳng tọa độ Oxy. Bằng quan sát, hãy chỉ ra một phép đối xứng trục f và một phép vị tự g sao cho phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép f và g (thực hiện f trước, g sau) biến hình ℋ thành hình ℋ ".
Bằng quan sát và đo đạc, hãy cho biết hai hình sau (H.1.55) có đồng dạng với nhau hay không.

Tranh Đông Hồ là một dòng tranh dân gian Việt Nam, xuất xứ từ làng Đông Hồ (xã Song Hồ, huyện Thuận Thành, tỉnh Bắc Ninh). Tranh được in trên giấy điệp, màu sắc được sử dụng là màu tự nhiên: màu đen từ than lá tre, màu xanh từ lá chàm, màu đỏ từ sỏi,... Nghề làm tranh dân gian Đông Hồ là di sản văn hóa phi vật thể cấp Quốc gia.
(Nguồn: https:vi.wikipedia.org/wki)

Ba bức tranh trong Hình 46 có hình dạng giống hệt nhau nhưng có kích thước to nhỏ khác nhau gợi nên những hình có mối liên hệ gì?
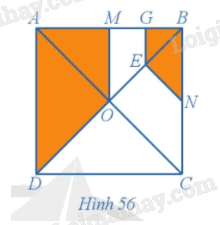
Trong Ví dụ 8, chứng minh rằng hai hình OMGE và COEN đồng dạng với nhau.
Người ta dùng một kính hiển vi có khả năng phóng to vật lên gấp 100 000 lần để quan sát một virus và đo được kích thước của virus là 2 mm. Hỏi kích thước thật của virus là bao nhiêu micromét (μm)?
Phép biến hình nào trong các phép biến hình dưới đây không là phép đồng dạng?
a) Phép đối xứng trục;
b) Phép đồng nhất;
c) Phép vị tự tỉ số \(k = 1\);
d) Phép biến hình biến mỗi điểm trong mặt phẳng thành điểm A cho trước.
Khẳng định nào dưới đây là đúng?
a) Hai tam giác luôn đồng dạng với nhau;
b) Hai hình chữ nhật luôn đồng dạng với nhau;
c) Hai hình thoi luôn đồng dạng với nhau;
d) Hai hình vuông luôn đồng dạng với nhau.
Trên bản đồ bay với tỉ lệ xích 1: 10 000 000, khoảng cách giữa Hà Nội và Tokyo đo được là 37,34 cm. Khoảng cách thực tế (tính theo đường chim bay) giữa Hà Nội và Tokyo là bao nhiêu kilômét?
Chứng minh rằng nếu phép đồng dạng F biến tam giác ABC thành tam giác A'B'C' thì F biến trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC thành trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác A'B'C'.
Chứng minh rằng các đa giác đều có cùng số cạnh thì đồng dạng với nhau.
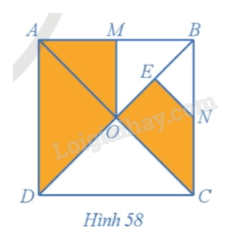
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Gọi M, N, E lần lượt là trung điểm của AB, BC, BO (Hình 58). Chứng minh rằng hai hình AMOD và OENC đồng dạng với nhau.
Hình 59 mô tả một viên gạch trang trí hình tam giác đều. Chứng minh rằng hình hoa ba cánh màu xanh và hình hoa ba cánh màu đỏ đồng dạng với nhau.

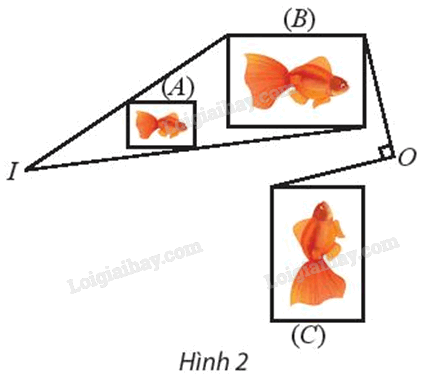
Tìm phép đồng dạng biến hình (A) thành hình (C).
Cho trước ba số thực a, b, k. Trong mặt phẳng tọa độ Oxy, xét phép biến hình g biến điểm M(x; y) thành điểm M’(x’; y’) thỏa mãn: \(\left\{ \begin{array}{l}x' = kx + a\\y' = ky + b\end{array} \right.\). Hãy chứng minh g là một phép đồng dạng.
Tìm các cặp hình đồng dạng với nhau có trong Hình 5.

Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
a) Gọi \({A_1}{B_1}{C_1}{Đ_1}\) là ảnh của hình vuông ABCD qua phép tịnh tiến theo vectơ . Gọi φ là góc lượng giác (O’A1, O’A’). Tìm ảnh \({A_2}{B_2}{C_2}{Đ_2}\) của hình vuông A1B1C1D1 qua phép quay \({Q_{\left( {O',{\rm{ }}\varphi } \right)}}.\)
b) Cho biết \(\overrightarrow {OA'} = k\overrightarrow {O{A_2}} \). Tìm ảnh của hình vuông \({A_2}{B_2}{C_2}{Đ_2}\) qua phép vị tự \({V_{\left( {O',{\rm{ }}k} \right)}}.\)
c) Từ kết quả của câu a) và b), hãy cho biết ta có thể kết luận là hai hình vuông tùy ý luôn đồng dạng với nhau được không. Giải thích.

Cho hình chữ nhật ABCD có AC cắt BD tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hình thang JLKI và hình thang IHDC đồng dạng với nhau.
Cho ∆ABC đều có cạnh bằng 2. Qua ba phép biến hình liên tiếp: Phép tịnh tiến, phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}},\) phép vị tự \({V_{\left( {A,{\rm{ }}3} \right)}},\)∆ABC biến thành \(\Delta {A_1}{B_1}{C_1}\). Tìm diện tích \(\Delta {A_1}{B_1}{C_1}\).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O bán kính R = 9 và cho điểm A khác O. Gọi (C’) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) và phép vị tự \({V_{\left( {O; - \frac{1}{3}} \right)}}\). Tìm diện tích hình tròn (C’).
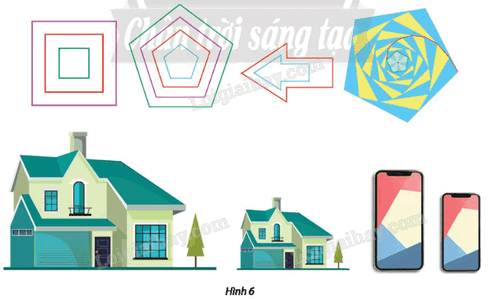
Tìm các hình đồng dạng với nhau trong Hình 6.







Danh sách bình luận