Trên một nửa mặt phẳng bờ chứa tia Ot và ba tia Ox, Oy, Oz sao cho \(\widehat {tOz} = 45^\circ ,\widehat {tOy} = 90^\circ ,\widehat {tOx} = 135^\circ \). Trong bốn tia Ot, Ox, Oy, Oz, tia nào nằm giữa hai tia trong ba tia còn lại? Tia Oy có phải là tia phân giác của góc xOz không? Vì sao?
Chứng minh trên một nửa mặt phẳng bờ chứa một tia, góc tạo bởi một tia với tia đã cho có số đo góc nhỏ hơn thì tia đó nằm giữa hai tia còn lại.
Để chứng minh tia phân giác thì ta chứng mình tia đó nằm giữa hai tia tạo ra góc và chia góc đó thành hai góc bằng nhau.
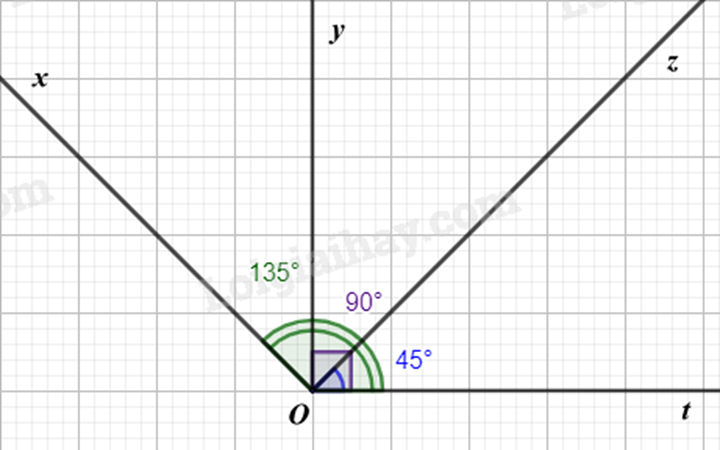
+ Trên một nửa mặt phẳng bờ chứa tia Ot có \(\widehat {tOz} = 45^\circ ;\widehat {tOy} = 90^\circ \).
Vì \(\widehat {tOz} < \widehat {tOy}\left( {45^\circ < 90^\circ } \right)\) nên Oz nằm giữa tia Ot và tia Oy.
Suy ra \(\widehat {tOz} + \widehat {zOy} = \widehat {tOy}\)
hay \(45^\circ + \widehat {zOy} = 90^\circ \)
suy ra \(\widehat {zOy} = 90^\circ - 45^\circ = 45^\circ \) (1)
+ Trên một nửa mặt phẳng bờ chứa tia Ot có \(\widehat {tOz} = 45^\circ ;\widehat {tOx} = 135^\circ \).
Vì \(\widehat {tOz} < \widehat {tOx}\left( {45^\circ < 135^\circ } \right)\) nên Oz nằm giữa tia Ot và tia Oy.
Suy ra \(\widehat {tOz} + \widehat {zOx} = \widehat {tOx}\)
hay \(45^\circ + \widehat {zOx} = 135^\circ \)
suy ra \(\widehat {zOx} = 135^\circ - 45^\circ = 90^\circ \) (2)
Từ (1) và (2) suy ra \(\widehat {zOy} < \widehat {zOx}\left( {45^\circ < 90^\circ } \right)\) nên Oy nằm giữa tia Oz và Ox.
suy ra \(\widehat {zOy} + \widehat {yOx} = \widehat {zOx}\)
hay \(45^\circ + \widehat {yOx} = 90^\circ \)
suy ra \(\widehat {yOx} = 90^\circ - 45^\circ = 45^\circ \)
+ Vì \(\widehat {zOy} = \widehat {yOx} = \frac{{\widehat {zOx}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \) và Oy nằm giữa tia Oz và Ox nên Oy là tia phân giác của góc xOz.
Lý thuyết liên quan
- Tia nằm giữa hai tia khác trên cùng một nửa mặt phẳng: Trên một nửa mặt phẳng có bờ chứa tia Ot, nếu tia Oz tạo với tia Ot một góc có số đo nhỏ hơn góc mà tia Oy tạo với tia Ot ($\widehat{tOz} < \widehat{tOy}$), thì tia Oz sẽ nằm giữa tia Ot và tia Oy.
- Quan hệ giữa các góc khi một tia nằm giữa hai tia khác: Nếu tia Oz nằm giữa tia Ot và tia Oy, thì tổng số đo của hai góc nhỏ kề nhau ($\widehat{tOz}$ và $\widehat{zOy}$) sẽ bằng số đo của góc lớn ($\widehat{tOy}$), tức là $\widehat{tOz} + \widehat{zOy} = \widehat{tOy}$.
- Tia phân giác của một góc: Tia phân giác của một góc là tia nằm giữa hai cạnh của góc đó và chia góc đó thành hai góc có số đo bằng nhau. Nếu tia Oy là tia phân giác của góc xOz, thì Oy phải nằm giữa hai tia Ox, Oz và $\widehat{xOy} = \widehat{yOz}$. Điều này cũng có nghĩa là $\widehat{xOy} = \widehat{yOz} = \frac{{\widehat {xOz}}}{2}$.
Phương pháp giải chung cho dạng bài
- Xác định tia nằm giữa hai tia cùng phía so với tia bờ:
- Liệt kê các góc được tạo bởi tia bờ chung (ví dụ: Ot) với các tia khác (Ox, Oy, Oz, ...).
- Trên cùng một nửa mặt phẳng có bờ chứa tia Ot, tia nào tạo với tia Ot góc có số đo nhỏ hơn thì tia đó nằm giữa tia Ot và tia tạo góc lớn hơn.
- Xác định tia nằm giữa hai tia bất kỳ (không nhất thiết phải có tia bờ):
- Tính số đo các góc tạo bởi ba tia cần xét (ví dụ: $\widehat{xOy}$, $\widehat{yOz}$, $\widehat{xOz}$). Áp dụng quy tắc cộng góc: nếu tia Ob nằm giữa tia Oa và tia Oc, thì $\widehat{aOb} + \widehat{bOc} = \widehat{aOc}$.
- Ngược lại, nếu ba tia Oa, Ob, Oc cùng nằm trên một nửa mặt phẳng bờ là đường thẳng chứa tia Oa, và $\widehat{aOb} + \widehat{bOc} = \widehat{aOc}$, thì tia Ob nằm giữa hai tia Oa và Oc.
- Kiểm tra tia phân giác:
- Để một tia (ví dụ: Oy) là tia phân giác của một góc (ví dụ: $\widehat{xOz}$), cần chứng minh hai điều kiện:
- Tia đó (Oy) nằm giữa hai cạnh của góc ($\widehat{xOz}$), tức là nằm giữa hai tia Ox và Oz. Sử dụng phương pháp ở bước 2 để chứng minh.
- Tia đó chia góc thành hai góc bằng nhau ($\widehat{xOy} = \widehat{yOz}$). Tính số đo các góc này và so sánh.
- Để một tia (ví dụ: Oy) là tia phân giác của một góc (ví dụ: $\widehat{xOz}$), cần chứng minh hai điều kiện:

Các bài tập cùng chuyên đề
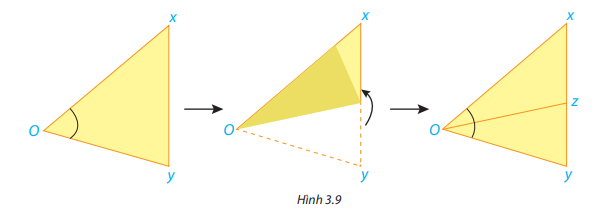
Cắt rời một góc xOy từ một tờ giấy rồi gấp sao cho hai cạnh của góc trùng nhau (H.3.9).
Mở mảnh giấy ra, nếp gấp cho ta hình ảnh tia Oz chia góc ban đầu thành hai góc.
a) Em hãy nhận xét về vị trí của tia Oz so với hai cạnh của góc xOy.
b) Em hãy so sánh hai góc xOz và zOy.
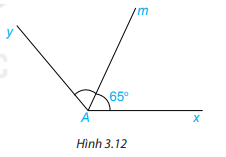
Cho góc xAm có số đo bằng \(65^\circ \) và Am là tia phân giác của góc xAy (H.3.12). Tính số đo góc xAy
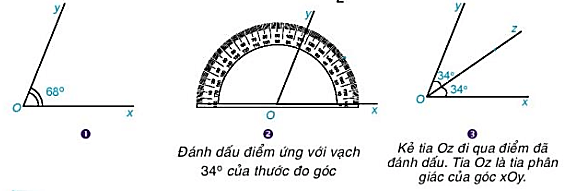
Vẽ tia phân giác Oz của xOy có số đo bằng 68\(^\circ \), sử dụng thước đo góc theo hướng dẫn. Nếu Oz là toa phân giác của góc xOy thì \(\widehat {xOz} = \frac{1}{2}.68^\circ = 34^\circ \). Ta có cách vẽ sau:
Quan sát hình vẽ bên.
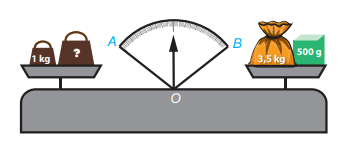
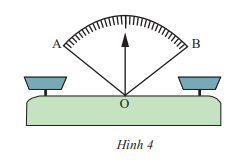
Quả cân ở đĩa cân bên trái nặng bao nhiêu kilogam để cân thăng bằng, tức là kim trên mặt đồng hồ của cân là tia phân giác của góc AOB?
Khi làm con diều như hình bên thì tia DB nằm ở vị trí nào của \(\widehat {ADC}\)?
Vẽ \(\widehat {xOy}\) lên một tờ giấy như trong hình 1a. Gấp giấy sao cho cạnh Oy trùng với cạnh Ox. Nếp gấp cho ta vị trí của tia Oz. Theo em, tia Oz đã chia\(\widehat {xOy}\) thành hai góc như thế nào?
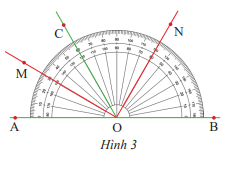
Tìm tia phân giác của các góc: \(\widehat {AOC}\) và \(\widehat {COB}\) trong hình 3.
Em hãy cho biết khi cân thăng bằng thì kim ở vị trí nào của \(\widehat {AOB}\)(Hình 4)
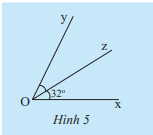
Trong Hình 5, nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì số đo của \(\widehat {xOy}\) bằng bao nhiêu?
Vẽ một góc có số đo bằng 60 \(^\circ \) rồi vẽ tia phân giác của góc đó.
Hãy vẽ một góc bẹt \(\widehat {AOB}\) rồi vẽ tia phân giác của góc đó.
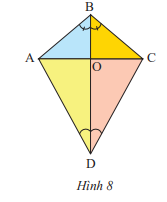
a) Trong Hình 8, tìm tia phân giác của góc \(\widehat {ABC},\widehat {ADC}\)
b) Cho biết \(\widehat {ABC} = 100^\circ ;\widehat {ADC} = 60^\circ \). Tính số đo của các góc \(\widehat {ABO},\widehat {ADO}\)
a) Vẽ \(\widehat {xOy}\) có số đo là 110\(^\circ \).
b) Vẽ tia phân giác của \(\widehat {xOy}\) trong câu a
Trong những câu sau, em hãy chọn những câu đúng.
Tia Oz là tia phân giác của góc \(\widehat {xOy}\) khi:
\(\begin{array}{l}a)\widehat {xOz} = \widehat {yOz}\\b)\widehat {xOz} + \widehat {yOz} = \widehat {xOy}\\c)\widehat {xOz} = \widehat {yOz} = \frac{{\widehat {xOy}}}{2}\end{array}\)
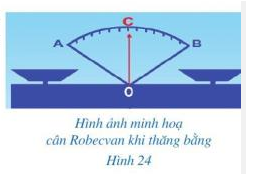
Hình 24 gợi nên hình ảnh tia OC nằm trong góc AOB và chia góc đó thành hai góc bằng nhau là AOC và BOC.
Tia OC được gọi là tia gì của góc AOB?
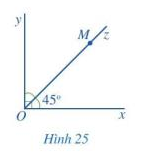
Quan sát góc vuông xOy và tia Oz ở Hình 25.
a) Mỗi điểm M (M khác O) thuộc tia Oz có phải là điểm trong của góc xOy hay không? Tia Oz có nằm trong góc xOy hay không?
b) Tính số đo góc yOz.
c) So sánh hai góc xOz và yOz.
Kiểm tra lại bằng thước đo góc để thấy góc xOC và yOC trong Hoạt động 2 là bằng nhau.
Kiểm tra lại bằng thước đo góc để thấy góc mIK và nIK trong Hoạt động 3 là bằng nhau
Để xác định phương hướng trên bản đồ hay trên thực địa, người ta thường xác định 8 hướng ( Bắc, Nam, Đông, Tây, Đông Bắc, Đông Nam, Tây Nam, Tây Bắc) như Hình 29. Trong đó:

a) Tia OB là tia phân giác của góc (khác góc bẹt) nào?
b) Tia OT là tia phân giác của góc (khác góc bẹt) nào?
Ở Hình 31 có góc vuông xOy, các tia On, Oz, Om nằm trong góc đó và \(\widehat {xOn} = \widehat {nOz},\widehat {yOm} = \widehat {mOz}\).
a) Các tia Om, On có tương ứng là tia phân giác của góc yOz và xOz hay không?
b) Cho biết số đo góc mOn.
Cho \(\widehat {xOy} = 120^\circ \). Vẽ tia phân giác của góc xOy bằng 2 cách:
a) Sử dụng thước thẳng và compa; b) Sử dụng thước hai lề
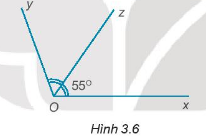
Cho hình 3.6. Biết tia Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {xOy}\).
Cho góc bẹt xOy. Vẽ tia Oz sao cho \(\widehat {xOz} = {60^0}\). Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.
a)Tính số đo góc xOm.
b) Tính số đo góc yOn.
c) Tính số đo góc mOn.
Vẽ \(\widehat {xOy} = {60^0}\). Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc zOy.
a) Tính \(\widehat {zOm}\).
b) Vẽ tia On là tia đối của tia Om. Tia Ox có phải là tia phân giác của góc yOn không? Vì sao?
Tia Ot là tia phân giác của \(\widehat {xOy}\). Khi đó
A. \(\widehat {xOt} > \widehat {tOy}\)
B. \(\widehat {xOt} = \widehat {tOy} = 2\widehat {xOy}\)
C. \(\widehat {xOt} = \frac{1}{2}\widehat {tOy}\)
D. \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy}\).
Vẽ \(\widehat {xOy} = {80^o}\). Vẽ tia Ot nằm giữa hai tia Ox và Oy sao cho \(\widehat {xOt} = {40^o}\). Chứng tỏ Ot là tia phân giác của góc xOy.
Cho \(\widehat {xOy}=30^o\); Oy là tia phân giác \(\widehat {xOy}\). Khi đó \(\widehat {xOz}\) bằng:
-
A.
90°;
-
B.
120°;
-
C.
15°;
-
D.
60°.
Tia Oz là tia phân giác của \(\widehat{xOy}\), biết rằng \(\widehat{xOz} = 40^\circ\). Số đo của \(\widehat{yOz}\) là:
-
A.
\(20^\circ\);
-
B.
\(40^\circ\);
-
C.
\(80^\circ\);
-
D.
\(140^\circ\).
Cho góc bẹt \( \widehat{aOb} \). Gọi Oc là tia phân giác của \( \widehat{aOb} \); Ox là phân giác của \( \widehat{aOc} \); Oy là phân giác của \( \widehat{cOb} \). Tính số đo \( \widehat{xOy} \).
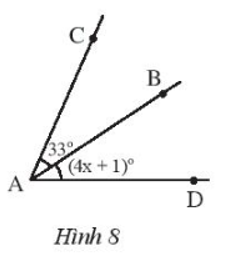
Cho biết AB là tia phân giác của \(\widehat {CAD}\).
Tìm giá trị của x.









Danh sách bình luận