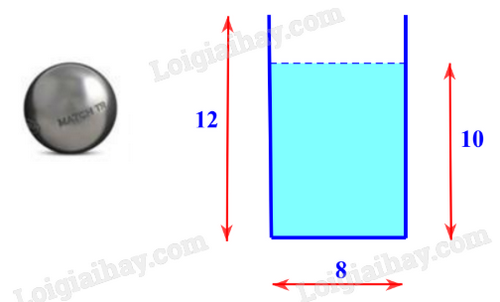
Một cốc nước có dạng hình trụ với đường kính đáy bằng 8 cm, chiều cao 12 cm và chứa một lượng nước cao 10 cm.
a) Tính thể tích lượng nước chứa trong cốc (làm tròn đến hàng phần trăm).
b) Người ta thả từ từ một viên bi làm bằng thép đặc (không thấm nước) có thể tích là \(4\pi \) \(\left( {c{m^3}} \right)\) vào trong cốc. Hỏi mực nước trong cốc lúc này là bao nhiêu cm?
a) Tính bán kính đáy cốc.
Tính thể tích lượng nước áp dụng công thức thể tích hình trụ \(V = \pi {r^2}h\).
b) Gọi \({h_1}\) là chiều cao nước dâng thêm.
Thể tích nước dâng thêm bằng thể tích viên bi nên ta tìm được \({h_1}\).
Mực nước hiện tại bằng \(h + {h_1}\).
a) Bán kính đáy cốc nước là r = 8 : 2 = 4 (cm); mực nước ban đầu là h = 10 (cm).
Thể tích lượng nước chứa trong cốc là \(V = \pi {r^2}h = \pi {.4^2}.10 = 160\pi \approx 502,65\) \(\left( {c{m^3}} \right)\).
b) Gọi \({h_1}\) là chiều cao nước dâng thêm.
Thể tích nước dâng thêm bằng thể tích viên bi nên \(\pi {r^2}{h_1} = 4\pi \)
\(\pi {.4^2}{h_1} = 4\pi \)
\({h_1} = 0,25\) (cm).
Vậy mực nước trong cốc sau khi thả viên bi là 10 + 0,25 = 10,25 (cm).
