Cho đường tròn (O;R) và dây MN cố định (MN < 2R). Kẻ đường kính AB vuông góc với dây MN tại E (điểm A thuộc cung nhỏ MN). Lấy điểm C thuộc dây MN (C khác M, N, E). Đường thẳng BC cắt (O;R) tại điểm K (K khác B).

a) Chứng minh AKCE là tứ giác nội tiếp.

b) Chứng minh \(B{M^2} = BK.BC\).

c) Gọi I là giao điểm của hai đường thẳng AK và MN; D là giao điểm của hai đường thẳng AC và BI. Chứng minh C cách đều ba cạnh của \(\Delta DEK\).

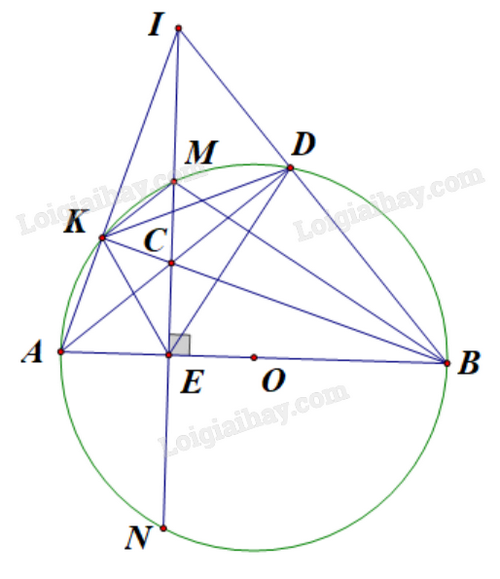
a) Vì K thuộc đường tròn đường kính AB nên \(\widehat {AKC} = {90^o}\).

Theo giả thiết, \(MN \bot AB\) nên \(\widehat {AEC} = {90^o}\).

Vì \(\widehat {AKC} = \widehat {AEC} = {90^o}\) nên K, E cùng thuộc đường tròn đường kính AC.

Vậy AKCE là tứ giác nội tiếp.

b) Vì AKCE là tứ giác nội tiếp nên \(\widehat {KAE} + \widehat {KCE} = {180^o}\).

Mặt khác, AKMB là tứ giác nội tiếp (O;R) nên \(\widehat {KAE} + \widehat {KMB} = {180^o}\).

Suy ra \(\widehat {KCE} = \widehat {KMB}\) (cùng bù với \(\widehat {KAE}\)); mà \(\widehat {KCE} = \widehat {MCB}\) (góc đối đỉnh) nên \(\widehat {KMB} = \widehat {MCB}\left( { = \widehat {KCE}} \right)\).

Xét \(\Delta BMK\) và \(\Delta BCM\) có:

+ \(\widehat {MBC}\) chung;

+ \(\widehat {KMB} = \widehat {MCB}\) (chứng minh trên).

Do đó $\Delta BMK\backsim \Delta BCM$ (g.g), suy ra \(\frac{{BM}}{{BC}} = \frac{{BK}}{{BM}}\), như vậy \(B{M^2} = BC.BK\).

c) Xét \(\Delta IAB\) có hai đường cao BK, IE cắt nhau tại C, do đó C là trực tâm \(\Delta IAB\).

Khi đó AD cũng là đường cao của \(\Delta IAB\), hay \(AD \bot IB\).

Vì \(\widehat {ADB} = {90^o}\) nên D thuộc đường tròn đường kính AB, hay D thuộc (O;R).

Vì tứ giác AKDB nội tiếp (O;R) nên \(\widehat {DKB} = \widehat {DAB}\) (góc nội tiếp cùng chắn cung BD).

Mà tứ giác AKCE nội tiếp (chứng minh trên) nên \(\widehat {BKE} = \widehat {DAB}\) (góc nội tiếp cùng chắn cung CE).

Suy ra \(\widehat {DKB} = \widehat {BKE}\left( { = \widehat {DAB}} \right)\) hay KB là phân giác của \(\widehat {DKE}\).

Vì \(\widehat {CDB} = \widehat {CEB} = {90^o}\) nên D, E thuộc đường tròn đường kính BC hay tứ giác BDCE nội tiếp.

Khi đó \(\widehat {EBC} = \widehat {EDC}\) (góc nội tiếp cùng chắn cung CE).

Mà tứ giác AKDB nội tiếp nên \(\widehat {EBC} = \widehat {CDK}\) (góc nội tiếp cùng chắn cung AK).

Suy ra \(\widehat {EDC} = \widehat {CDK}\left( { = \widehat {EBC}} \right)\) hay DC là phân giác của \(\widehat {KDE}\).

Xét \(\Delta DEK\) có các đường phân giác góc \(\widehat {DKE}\), \(\widehat {KDE}\) cắt nhau tại C.

Do đó, C là tâm đường tròn nội tiếp \(\Delta DEK\), hay C cách đều các cạnh của \(\Delta DEK\).