Thiết kế khu vườn Hạnh Phúc hình vuông cạnh 10 m như hình vẽ.
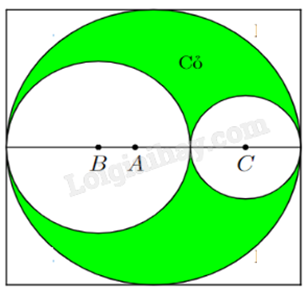
Phần được tô đậm dùng để trồng cỏ, phần còn lại lát gạch. Biết mỗi mét vuông trồng cỏ chi phí 100 nghìn đồng, mỗi mét vuông lát gạch chi phí 300 nghìn đồng. Khi diện tích phần lát gạch là nhỏ nhất thì tổng chi phí thi công vườn hoa Hạnh Phúc bằng bao nhiêu triệu đồng (làm tròn đến hàng triệu)?
Gọi x, y lần lượt là bán kính của phần lát gạch hình tròn (mét; x, y > 0).
S là phần diện tích được lát gạch của khu vườn (mét vuông; S > 0).
(O;R) là đường tròn lớn được tô đậm.
\(\Delta \) là đường thẳng x + y – 5 = 0.
Bài toán trở thành: Tìm R nhỏ nhất để (O;R) và \(\Delta \) có ít nhất một điểm chung, với hoành độ và tung độ đều là các số dương.
Gọi x, y lần lượt là bán kính của phần lát gạch hình tròn (mét; x, y > 0).
S là phần diện tích được lát gạch của khu vườn (mét vuông; S > 0).
\(S = 100 - 25\pi + \pi {x^2} + \pi {y^2} = 100 + \pi \left( {{x^2} + {y^2} - 25} \right)\)
\( \Leftrightarrow {x^2} + {y^2} = \frac{{S + 25\pi - 100}}{\pi }\).
Gọi (O;R) là đường tròn lớn được tô đậm.
Khi đó (O;R) có phương trình \({x^2} + {y^2} = \frac{{S + 25\pi - 100}}{\pi }\) với tâm O(0;0) và bán kính \(R = \sqrt {\frac{{S + 25\pi - 100}}{\pi }} \).
Gọi \(\Delta \) là đường thẳng x + y – 5 = 0.
Bài toán trở thành: Tìm R nhỏ nhất để (O;R) và \(\Delta \) có ít nhất một điểm chung, với hoành độ và tung độ đều là các số dương.

(O;R) và \(\Delta \) có ít nhất một điểm chung khi và chỉ khi:
\(R \ge d\left( {O,\Delta } \right) \Leftrightarrow \sqrt {\frac{{S + 25\pi - 100}}{\pi }} \ge \frac{5}{{\sqrt 2 }}\)
\( \Leftrightarrow S + 25\pi - 100 \ge \frac{{25\pi }}{2}\)
\( \Leftrightarrow S \ge 100 - \frac{{25\pi }}{2}\).
Vậy diện tích phần lát gạch nhỏ nhất bằng\({S_{\min }} = 100 - \frac{{25\pi }}{2}\).
Chi phi để thi công khu vườn là:
\(100(100 - {S_{\min }}) + 300.{S_{\min }} \approx 22146\) nghìn đồng \( \approx 22\) triệu đồng.

Các bài tập cùng chuyên đề
Bên trong một hồ bơi, người ta dự định thiết kế hai bể sục nửa hình tròn bằng nhau và một bể sục hình tròn (H7.14) để người bơi có thể ngồi tựa lưng vào thành các bề sục thư giãn. Hãy tìm bán kính của các bể sục đề tồng chu Vị của ba bể là 32 m mà tổng diện tích (chiếm hồ bơi) là nhỏ nhất. Trong tính toán, lấy 13, 14, độ dài tính theo mét và làm tròn tới chữ số thập phân thứ hai.
Viết phương trình đường tròn \(\left( C \right)\) đi qua ba điểm \(M\left( {4; - 5} \right),N\left( {2; - 1} \right),P\left( {3; - 8} \right)\).
Hãy cho biết phương trình nào dưới đây là phương trình đường tròn. Tìm tâm và bán kính của đường tròn đó.
a) \({x^2} - {y^2} - 2x + 4y - 1 = 0\)
b) \({x^2} + {y^2} - 2x + 4y + 6 = 0\)
c) \({x^2} + {y^2} + 6x - 4y + 2 = 0\)
Tìm tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} = 7\).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C), tâm I(a;b), bán kính R (H.7.13). Khi đó, một điểm M(x;y) thuộc đường tròn (C) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện đại số nào?
Tìm tâm và bán kính của đường tròn \({\left( {x + 3} \right)^2} + {\left( {y - 3} \right)^2} = 36\).
Hãy cho biết phương trình nào dưới đây là phương trình đường tròn, tìm tâm và bán kính của đường tròn đó.
a) \({x^2} + {y^2} + xy + 4x - 2 = 0\)
b) \({x^2} + {y^2} - 2x - 4y + 5 = 0\)
c) \({x^2} + {y^2} + 6x - 8y + 1 = 0\)
Viết phương trình của đường tròn (C) trong mỗi trường hợp sau:
a) Có tâm I(-2; 5) và bán kính R= 7;
b) Có tâm I(1;-2) và đi qua điểm A(-2, 2);
c) Có đường kính AB, với A(-1; -3), B(-3; 5);
d) Có tâm I(1; 3) và tiếp xúc với đường thẳng x+2y +3 = 0.
Trong mặt phẳng toạ độ, cho tam giác ABC, với A(6; -2), B(4; 2), C(5; -5). Viết phương trình đường tròn ngoại tiếp tam giác đó.
Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng toạ độ. Theo đó, tại thời điểm t (\[0{\rm{ }} \le t \le 180\] ) vật thể ở vị trí có toạ độ \(\left( {2{\rm{ }} + {\rm{ }}sin{t^o};{\rm{ }}4{\rm{ }} + {\rm{ }}cos{t^o}} \right)\).
a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể.
b) Tìm quỹ đạo chuyển động của vật thể.
Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} - {y^2} = 1\)
B. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = - 4\)
C. \({x^2} + {y^2} = 2\)
D. \({y^2} = 8x\)
Một sân khấu đã được thiết lập một hệ trục tọa độ bởi đạo diễn có thể sắp đặt ánh sáng và xác định vị trí của các diễn viên. Cho biết một đèn chiếu đang gọi trên sân khấu một vùng sáng bên trong đường tròn (C) có phương trình \({\left( {x - 13} \right)^2} + {\left( {y - 4} \right)^2} = 16\).
a) Tìm tọa độ tâm và bán kính của đường tròn (C).
b) Cho biết tọa độ trên sân khấu của 3 diễn viên A, B, C như sau: \(A(11;4).B(8;5),C(15;5)\).Diễn viên nào đang được đèn chiếu sáng?
Theo dữ kiện đã cho trong hoạt động khởi động của bài học, viết phương trình đường tròn biểu diễn tập hợp các điểm xa nhất mà vòi nước có thể phun tới.
Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.
a) \({x^2} + {y^2} - 2x - 4y - 20 = 0\)
b) \({\left( {x + 5} \right)^2} + {\left( {y + 1} \right)^2} = 121\)
c) \({x^2} + {y^2} - 4x - 8y + 5 = 0\)
d) \(2{x^2} + 2{y^2} + 6x + 8y - 2 = 0\)
Viết phương trình đường tròn (C) trong các trường hợp sau:
a) (C) có tâm \(O\left( {0;0} \right)\), bán kính \(R = 4\)
b) (C) có tâm \(I\left( {2; - 2} \right)\), bán kính \(R = 8\)
c) (C) đi qua 3 điểm \(A(1;4),B(0;1),C(4;3)\)
Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.
a) \({x^2} + {y^2} - 6x - 8y + 21 = 0\)
b) \({x^2} + {y^2} - 2x + 4y + 2 = 0\)
c) \({x^2} + {y^2} - 3x + 2y + 7 = 0\)
d) \(2{x^2} + 2{y^2} + x + y - 1 = 0\)
Lập phương trình đường tròn trong các trường hợp sau:
a) \((C)\) có tâm \(I(1;5)\) và bán kính \(r = 4\)
b) \((C)\) có đường kính MN với \(M(3; - 1)\)và \(N(9;3)\)
c) \((C)\) có tâm \(I(2;1)\) và tiếp xúc với đường thẳng \(5x - 12y + 12 = 0\)
d) \((C)\) có tâm \(A(1; - 2)\) và đi qua điểm \(B(4; - 5)\)
Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là:
a) \(M(2;5),N(1;2),P(5;4)\)
b) \(A(0;6),B(7;7),C(8;0)\)
Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và đi qua điểm \(A(4;2)\).
Một cái cầu hình bán nguyệt rộng 8,4 m cao 4,2 m như hình 5. Mặt đường dưới cộng được chia thành hai làn cho xe ra vào.
a) Vết phương trình mô phỏng cái cổng.
b) Một chiếc xe tải rộng 2,2 m và cao 2,6 m đi đúng làn đường quy định có thể đi qua cổng và không làm hư hỏng cổng hay không?

Tìm tâm và bán kính của các đường tròn có phương trình:
a) \({\left( {x - 2} \right)^2} + {\left( {y - 7} \right)^2} = 64\)
b) \({\left( {x + 3} \right)^2} + {\left( {y + 2} \right)^2} = 8\)
c) \({x^2} + {y^2} - 4x - 6y - 12 = 0\)
Lập phương trình đường tròn trong các trường hợp sau:
a) Có tâm \(I( - 2;4)\) và bán kính bằng 9.
b) Có tâm \(I(1;2)\) và đi qua điểm \(A(4;5)\).
c) Đi qua hai điểm \(A(4;1),B(6;5)\) và có tâm nằm trên đường thẳng \(4x + y - 16 = 0\).
d) Đi qua gốc tọa độ và cắt 2 trục tọa độ tại các điểm có hoành độ a và tung độ là b.
Lập phương trình đường tròn đi qua ba điểm A(1; 2), B(5; 2), C(1 ; – 3).
Tìm k sao cho phương trình:\({x^2} + {y^2} + 2kx + 4y + 6k-1 = 0\) là phương trình đường tròn.
Viết phương trình đường tròn tâm I(6 ; - 4) đi qua điểm A(8 ; – 7).
Viết phương trình đường tròn (C): \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) về dạng \({x^2} + {y^2} - 2{\rm{a}}x - 2by + c = 0\).
Trong mặt phẳng toạ độ Oxy, nêu mối liên hệ giữa x và y để:
a) Điểm M(x ; y) nằm trên đường tròn tâm O(0 : 0) bán kính 5.
b) Điểm M(x ; y) nằm trên đường tròn (C) tâm I(a; b) bán kính R.
a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy.
b) Cho hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.
Ở một số công viên, người ta dựng vòng quay có bán kính rất lớn đặt theo phương thẳng đứng như Hình 42. Khi vòng quay hoạt động, một người ngồi trong cabin sẽ chuyển động theo đường tròn.
Làm thế nào để xác định được phương trình quỹ đạo chuyển động của người đó?
Phương trình nào sau đây là phương trình đường tròn?
a) \({x^2} + {y^2} - 2x + 2y - 7 = 0\)
b) \({x^2} + {y^2} - 8x + 2y + 20 = 0\)







Danh sách bình luận