Cho đa thức \(A\left( x \right) = 6{x^3} - 7{x^2} - x + m\) và \(B\left( x \right) = 2x + 1\)
a) Thực hiện phép chia \(A\left( x \right)\) cho \(B\left( x \right)\).
b) Tìm giá trị của \(m\) để phép chia trên có dư là \(4\).
Với hai đa thức một biến \(A\) và \(B\)(\(B\) khác đa thức \(0\)) tuỳ ý. Tồn tại hai đa thức duy nhất \(Q\) và \(R\) sao cho:
\(A = B.Q + R\) trong đó bậc của \(R\) thấp hơn bậc của \(B\)
A: đa thức bị chia
B: Đa thức chia
Q: Đa thức thương
\(R\): Đa thức dư
a) Ta thực hiện phép chia \(A\left( x \right):B\left( x \right)\)
Vậy \(\left( {6{x^3} - 7{x^2} - x + m} \right):\left( {2x + 1} \right)\) được thương là \(3{x^2} - 5x + 2\) dư \(m - 2\)
b) Để \(A\left( x \right):B\left( x \right)\) dư \(4\) thì \(m - 2 = 4 \Leftrightarrow m = 6\)
Vậy khi \(m = 6\) thì \(A\left( x \right):B\left( x \right)\) dư \(4\).


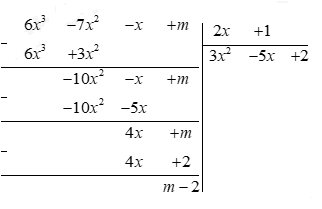






Danh sách bình luận