Cho tam giác ABC vuông tại A.
a) Tia phân giác của góc B cắt cạnh AC ở D. Kẻ DE vuông góc với BC tại E.
Chứng minh rằng ΔABD = ΔEBD.
b) So sánh AD và DC.
c) Tia ED cắt BA tại G. Gọi I là trung điểm GC. Chứng minh rằng B, D, I thẳng hàng.
Sử dụng tính chất tia phân giác, các phương pháp chứng minh hai tam giác vuông bằng nhau, mối quan hệ giữa cạnh và góc trong tam giác, tính chất của tam giác cân.
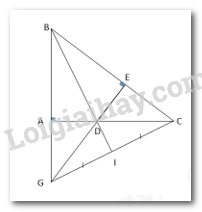
a) Chứng minh rằng ΔABD = ΔEBD.
Xét hai tam giác vuông ΔABD và ΔEBD ta có:
\(\widehat {A} =\widehat {E}=\widehat {90^0}\)
AD = DE (vì BD là tia phân giác)
BD cạnh chung
Suy ra ΔABD = ΔEBD (cạnh huyền – cạnh góc vuông) \( \Rightarrow \)AD = DE, BA = BE (cạnh tương ứng) (1)
b) So sánh AD và DC
Xét ΔDEC vuông tại E ta có: DC > DE
Lại có AD = DE (cmt)
\( \Rightarrow \)DC > AD
c) Chứng minh rằng B, D, I thẳng hàng.
Xét ΔBGC có AC \( \bot \) AB, GE \( \bot \) AC
Suy ra D là trực tâm của ΔBGC.(2)
Xét hai tam giác vuông ΔADG và ΔEDC ta có:
\(\widehat {ADG} =\widehat {EDC}\) (đối đỉnh)
\(\widehat {A} =\widehat {E}=\widehat {90^0}\)
AD = DE (cm câu b))
Suy ra ΔADG = ΔEDC (cạnh gv – góc nhọn)
\( \Rightarrow \)AG = EC (cạnh tương ứng) (3)
từ (1), (3) suy ra BA +AG = BE + EC\( \Leftrightarrow \) BG = BC
Vậy ΔBGC là tam giác cân tại B. (4)
từ (2), (4) suy ra BD là đường trung tuyến của tam giác ΔBGC. Hay B, D, I thẳng hàng. (đpcm)








Danh sách bình luận