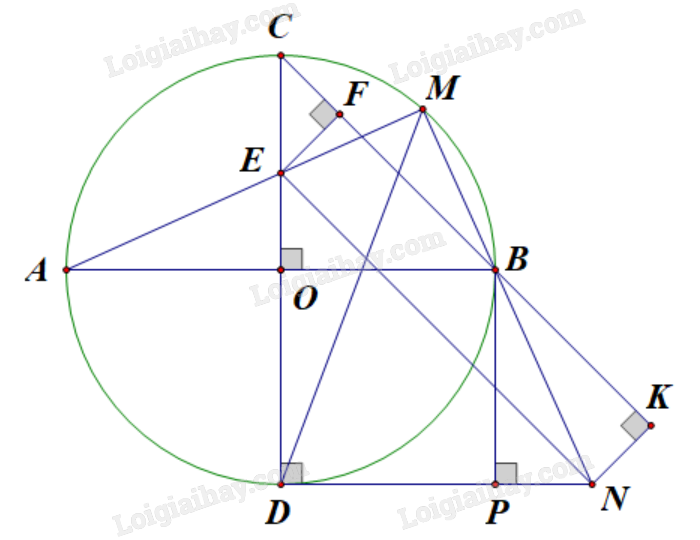
Cho (O) đường kính AB. Kẻ đường kính CD vuông góc với AB. Lấy M thuộc cung nhỏ BC, AM cắt CD tại E. Qua D kẻ tiếp tuyến với (O) cắt đường thẳng BM tại N. Gọi P là hình chiếu vuông góc của B lên DN.
a) Chứng minh các điểm M, N, D, E cùng thuộc một đường tròn.
b) Chứng minh EN // CB.
c) Chứng minh \(AB.BN = 2{R^2}\) và tìm vị trí điểm M trên cung nhỏ BC để diện tích tam giác BNC đạt giá trị lớn nhất.
a) Chứng minh \(\widehat {AMB} = \widehat {EMN} = {90^o}\).
b) Chứng minh \(\widehat {DEN} = \widehat {DCB}\).
c)
- Để chứng minh \(AB.BN = 2{R^2}\):
+ Chứng minh \(\widehat {MBA} = \widehat {PNB}\), suy ra , từ đó được \(\frac{{AM}}{{BP}} = \frac{{AB}}{{BN}}\)
+ Chứng minh OBPD là hình vuông, suy ra BP = OB = R.
+ Biến đổi các đẳng thức trên và kết luận.
- Để tìm M trên cung nhỏ BC sao cho diện tích tam giác BNC đạt giá trị lớn nhất:
+ Kẻ \(EF \bot BC\), \(NK \bot BC\) (F, K thuộc đường thẳng BC). Chứng minh EF = NK.dê
+ \({S_{NBC}} = \frac{1}{2}BC.NK\) max khi EF = NK max.
+ Kết luận vị trí điểm M.
a) Vì M thuộc đường tròn (O) đường kính AB nên \(\widehat {AMB} = \widehat {EMN} = {90^o}\).
Mặt khác, DN là tiếp tuyến của (O) tại D nên đường kính \(CD \bot DN\), do đó \(\widehat {EDN} = {90^o}\).
Có \(\widehat {EMN} = \widehat {EDN} = {90^o}\) nên D, M cùng thuộc đường tròn đường kính EN.
Vậy M, N, E, D cùng thuộc một đường tròn.
b) Vì tứ giác MNDE nội tiếp (chứng minh trên) nên \(\widehat {DEN} = \widehat {DMN}\) (góc nội tiếp cùng chắn cung DN).
Mặt khác, xét (O) có \(\widehat {DMB} = \widehat {DCB}\).
Do đó \(\widehat {DEN} = \widehat {DCB}\), mà hai góc trên ở vị trí đồng vị nên EN // BC.
c) Xét tứ giác OBPD có OB // DP (cùng vuông góc với CD), OD // BP (cùng vuông góc với DN) suy ra OBPD là hình bình hành.
Mặt khác, \(\widehat {BOD} = {90^o}\) và OB = OD nên OBPD là hình vuông, suy ra BP = OB = R.
Ta có AB // DN (cùng vuông góc với CD) nên \(\widehat {MBA} = \widehat {PNB}\) (góc đồng vị).
Xét \(\Delta MBA\) và \(\Delta PNB\):
+ \(\widehat {MBA} = \widehat {PNB}\) (chứng minh trên);
+ \(\widehat {AMB} = \widehat {BPN} = {90^o}\).
Do đó (g.g), suy ra \(\frac{{AM}}{{BP}} = \frac{{AB}}{{BN}}\)
\(AM.BN = AB.BP\)
\(AM.BN = 2R.R\)
\(AM.BN = 2{R^2}\) (đpcm).
Kẻ \(EF \bot BC\), \(NK \bot BC\) (F, K thuộc đường thẳng BC).
Xét từ giác EFKN có EN // FK, EF // NK (cùng vuông góc với BC), do đó EFKN là hình bình hành.
Mặt khác, \(\widehat {EFK} = {90^o}\) nên EFKN là hình chữ nhật, suy ra EF = NK.
Diện tích tam giác NBC là \({S_{NBC}} = \frac{1}{2}BC.NK\).
Do BC không đổi nên \({S_{NBC}}\) max khi và chỉ khi NK = EF max. Khi đó, E trùng O và M trùng B.
Vậy, để diện tích tam giác NBC lớn nhất thì M trùng B.








Danh sách bình luận