Một miếng tôn phẳng hình vuông với kích thước a (cm), người ta muốn cắt đi ở bốn góc bốn hình vuông cạnh bằng x (cm) để uốn thành một hình hộp chữ nhật không có nắp. Phải cắt như thế nào để hình hộp có thể tích lớn nhất?
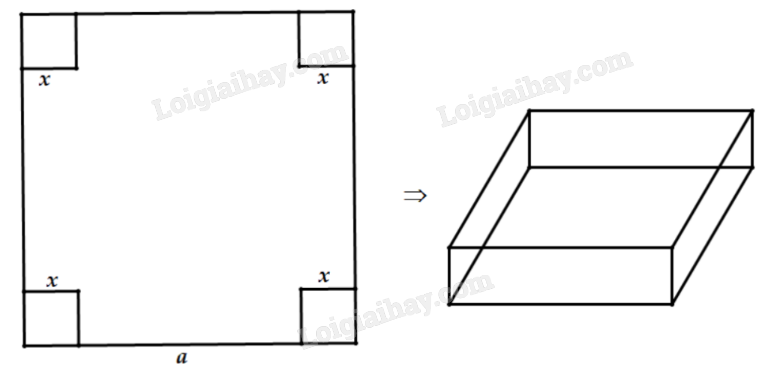
Biểu diễn thể tích hình hộp sau khi cắt góc theo x.
Áp dụng bất đẳng thức Cauchy cho ba số dương, tìm x.
Vì cạnh hình vuông bị cắt là x (cm) nên ta có điều kiện: 0 < x < a (cm).
Chiều dài cạnh miếng tôn sau khi cắt là a – 2x (cm), chiều cao hộp là x (cm).
Thể tích hình hộp là \(V = x(a - 2x)(a - 2x) = \frac{1}{4}4x(a - 2x)(a - 2x)\) \((c{m^3})\).
Áp dụng bất đẳng thức Cauchy cho ba số dương, ta có:
\(4x(a - 2x)(a - 2x) \le {\left( {\frac{{4x + a - 2x + a - 2x}}{3}} \right)^3}\)
\(\frac{1}{4}4x(a - 2x)(a - 2x) \le \frac{1}{4}{\left( {\frac{{2a}}{3}} \right)^3}\)
\(S \le \frac{{2{a^3}}}{{27}}\).
Dấu “=” xảy ra khi 4x = a – 2x, suy ra \(x = \frac{a}{6}\) (cm).
Vậy để thể tích hộp lớn nhất, cần cắt 4 góc hình vuông cạnh \(\frac{a}{6}\) (cm).







