Cho đường tròn (O), dây CD cố định. Gọi B là điểm chính giữa cung nhỏ CD, kẻ đường kính AB cắt CD tại I. Lấy điểm H bất kì trên cung lớn CD, HB cắt CD tại E. Đường thẳng AH cắt CD tại P.
a) Chứng minh tứ giác PHIB nội tiếp.
b) Chứng minh AH.AP = AI.AB.
c) Gọi K là giao điểm của đường thẳng AE và BP. Kẻ \(KM \bot AB\), cắt AB tại M, cắt đường tròn (O) tại N. Chứng minh N, I, H thẳng hàng.
a) Chứng minh \(\widehat {PIB} = \widehat {PHB} = {90^o}\).
b) Chứng minh (g.g), suy ra \(\frac{{AB}}{{AH}} = \frac{{AP}}{{AI}}\) rồi kết luận.
c) Chứng minh \(\widehat {HIP} = \widehat {DIN}\), suy ra \(\widehat {PIN} + \widehat {HIP} = {180^o}\) rồi kết luận.
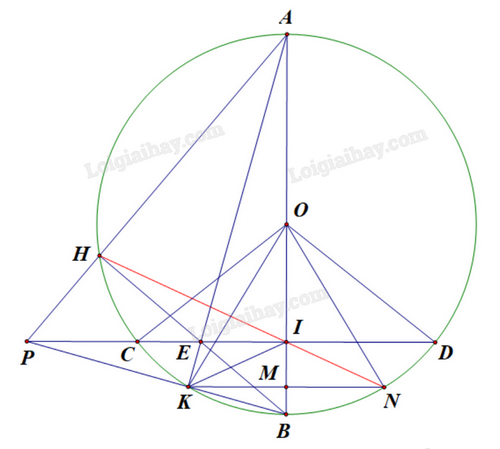
a) Vì B là điểm chính giữa cung nhỏ CD nên B cách đều C và D.
Mà C, D thuộc (O) nên O cũng cách đều C và D.
Do đó, OB là đường trung trực của đoạn thẳng CD, suy ra \(\widehat {PIB} = {90^o}\).
Vì vậy, I thuộc đường tròn đường kính PB.
Mặt khác, H thuộc đường tròn (O) đường kính AB nên \(\widehat {BHA} = \widehat {BHP} = {90^o}\).
Do đó, H thuộc đường tròn đường kính PB.
Vì I, H cùng thuộc đường tròn đường kính PB nên tứ giác PHIB nội tiếp.
b) Tứ giác PHIB nội tiếp nên \(\widehat {HPB} + \widehat {HIB} = {180^o}\), mà \(\widehat {AIH} + \widehat {HIB} = {180^o}\) (góc kề bù), suy ra \(\widehat {HPB} = \widehat {AIH}\).
Xét \(\Delta ABP\) và \(\Delta AHI\) có:
+ \(\widehat {HAI}\) chung;
+ \(\widehat {APB} = \widehat {AIH}\) (chứng minh trên).
Suy ra (g.g), do đó \(\frac{{AB}}{{AH}} = \frac{{AP}}{{AI}}\), vì vậy AH.AP = AI.AB.
c) Xét \(\Delta APB\) có hai đường cao PI và BH cắt nhau tại E, do đó E là trực tâm \(\Delta APB\).
Suy ra AK cũng là đường cao của \(\Delta APB\), do đó \(\widehat {AKB} = {90^o}\) và K thuộc (O).
Ta có \(\widehat {EKB} = \widehat {EIB} = {90^o}\) nên K, I cùng thuộc đường tròn đường kính EB, hay tứ giác EIBK nội tiếp.
Suy ra \(\widehat {EBK} = \widehat {EIK}\) (góc nội tiếp cùng chắn cung EK).
Mặt khác, do tứ giác PHIB nội tiếp nên \(\widehat {EBK} = \widehat {HIP}\) (góc nội tiếp cùng chắn cung PH).
Suy ra \(\widehat {EIK} = \widehat {HIP}\) (1)
Xét \(\Delta OKN\) cân tại O có OM là đường cao, do đó OM đồng thời là đường trung trực của đoạn KN.
Vì I thuộc đường trung trực OM của đoạn thẳng KN nên IK = IN, suy ra \(\Delta IKN\) cân tại I.
\(\Delta IKN\) cân tại I có IM là đường trung tuyến, đồng thời là phân giác của \(\widehat {KIN}\).
Do đó \(\widehat {KIM} = \widehat {NIM}\), suy ra \({90^o} - \widehat {KIM} = {90^o} - \widehat {NIM}\), ta được \(\widehat {EIK} = \widehat {DIN}\) (2)
Từ (1) và (2) suy ra \(\widehat {HIP} = \widehat {DIN}\).
Mặt khác \(\widehat {PIN} + \widehat {DIN} = {180^o}\) (góc kề bù), suy ra \(\widehat {PIN} + \widehat {HIP} = {180^o}\), hay \(\widehat {HIN} = {180^o}\).
Vậy H, I, N thẳng hàng.








Danh sách bình luận