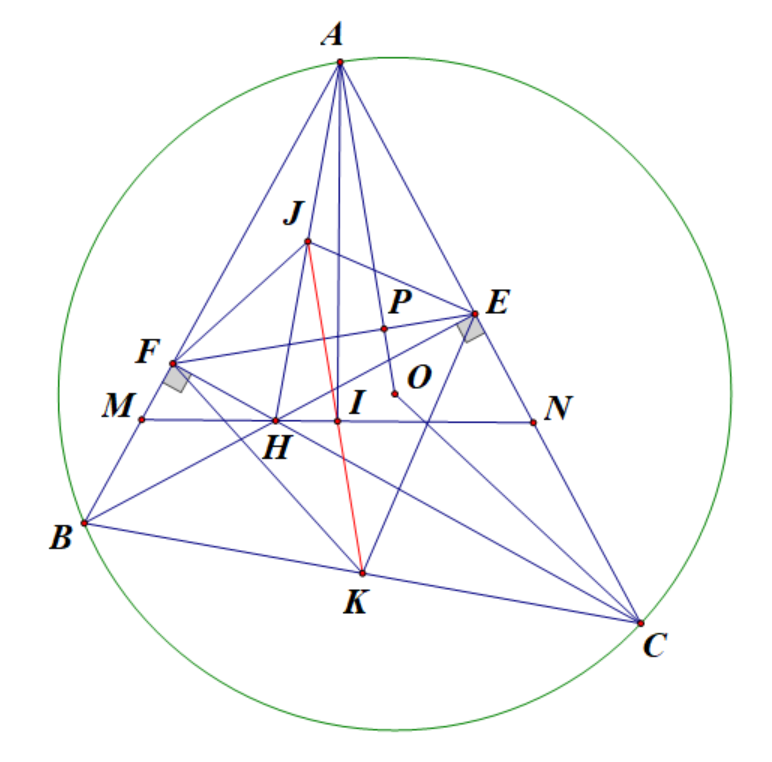
2) Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Hai đường cao BE và CF của tam giác ABC cắt nhau tại điểm H. Gọi K là trung điểm của BC.

a) Chứng minh \(\Delta AEF\) đồng dạng \(\Delta ABC\).

b) Chứng minh đường thẳng OA vuông góc với đường thẳng EF.

c) Đường phân giác góc FHB cắt AB và AC lần lượt tại M và N. Gọi I là trung điểm của MN, J là trung điểm của AH. Chứng minh tứ giác AFHI nội tiếp và ba điểm I, J, K thẳng hàng.

a) Vì BE, CF là hai đường cao của \(\Delta ABC\) nên \(\widehat {BFC} = \widehat {BEC} = {90^o}\).

Do đó, E, F cùng thuộc đường tròn đường kính BC, tức tứ giác BFEC nội tiếp.

Suy ra \(\widehat {FBC} + \widehat {FEC} = {180^o}\); mà \(\widehat {FEA} + \widehat {FEC} = {180^o}\) (góc kề bù) nên \(\widehat {FBC} = \widehat {AEF}\).

Xét \(\Delta AEF\) và \(\Delta ABC\) có:

\(\widehat {BAC}\) chung;

\(\widehat {FBC} = \widehat {AEF}\) (chứng minh trên).

Suy ra  (g.g).

b) Gọi P là giao điểm của AO và EF.

Ta có \(\widehat {ABC} = \frac{1}{2}\widehat {AOC}\) vì \(\widehat {ABC}\) là góc nội tiếp và \(\widehat {AOC}\) là góc ở tâm cùng chắn cung AC.

Vì A, C cùng thuộc đường tròn tâm O nên OA = OC, suy ra \(\Delta OAC\) cân tại O.

Do đó \(\widehat {EAO} = \frac{{{{180}^o} - \widehat {AOC}}}{2} = \frac{{{{180}^o}}}{2} - \frac{{\widehat {AOC}}}{2} = {90^o} - \widehat {ABC}\).

Mà \(\widehat {ABC} = \widehat {AEF}\) nên \(\widehat {EAO} = {90^o} - \widehat {AEF}\), suy ra \(\widehat {EAO} + \widehat {AEF} = {90^o}\) hay \(\widehat {EAP} + \widehat {AEP} = {90^o}\).

Xét \(\Delta APE\) có: \(\widehat {APE} + \widehat {EAP} + \widehat {AEP} = {180^o}\)

+ \(\widehat {APE} + {90^o} = {180^o}\)

+ \(\widehat {APE} = {90^o}\).

Vậy \(AO \bot EF\).

c) Vì HM là phân giác của \(\widehat {FHB}\) nên \(\widehat {MHB} = \frac{1}{2}\widehat {FHB}\).

Vì HN là phân giác của \(\widehat {EHC}\) nên \(\widehat {NHC} = \frac{1}{2}\widehat {EHC}\).

Mà \(\widehat {FHB} = \widehat {EHC}\) (góc đối đỉnh) nên \(\widehat {MHB} = \widehat {NHC}\).

Ta có:

+ \(\widehat {MBH} + \widehat {MHB} = \widehat {AMN}\) (cùng bù với \(\widehat {HMB}\));

+ \(\widehat {NCH} + \widehat {NHC} = \widehat {ANM}\) (cùng bù với \(\widehat {HNC}\));

+ \(\widehat {MHB} = \widehat {NHC}\) (chứng minh trên);

+ \(\widehat {MBH} = \widehat {NCH}\) (góc nội tiếp cùng chắn cung EF).

Suy ra \(\widehat {AMN} = \widehat {ANM}\), do đó \(\Delta AMN\) cân tại A.

Mà I là trung điểm của MN nên AI vừa là đường trung tuyến, vừa là đường cao của \(\Delta AMN\), suy ra \(AI \bot MN\).

Ta có \(\widehat {AFH} = \widehat {AIH} = {90^o}\) nên F, I cùng thuộc đường tròn đường kính AH, hay tứ giác AFHI nội tiếp.

Suy ra \(\widehat {FAH} = \widehat {FEH}\) (góc nội tiếp cùng chắn cung FH) (1)

Ta có:

+ \(\widehat {PAE} + \widehat {PEA} = {90^o}\);

+ \(\widehat {FEH} + \widehat {PEA} = {90^o}\).

Suy ra \(\widehat {PAE} = \widehat {FEH}\) (2)

Từ (1) và (2) suy ra \(\widehat {FAH} = \widehat {PAE}\) (3)

Ta có AI là đường cao đồng thời là đường phân giác của \(\Delta AMN\) cân tại A nên \(\widehat {MAI} = \widehat {NAI}\), suy ra \(\widehat {FAH} + \widehat {HAI} = \widehat {PAE} + \widehat {PAI}\) (4)

Từ (3) và (4) suy ra \(\widehat {HAI} = \widehat {PAI}\) (5)

Vì \(\Delta HAI\) vuông tại I có đường trung tuyến IJ ứng với cạnh huyền nên JA = JI, do đó \(\Delta AJI\) cân tại J, suy ra \(\widehat {HAI} = \widehat {JIA}\) (6)

Từ (5) và (6) suy ra \(\widehat {JIA} = \widehat {PAI}\), mà hai góc trên ở vị trí so le trong nên JI // AO.

Mà \(AO \bot EF\) nên \(IJ \bot EF\) (*)

Ta có \(\widehat {AFH} = \widehat {AEH} = {90^o}\) nên F, E cùng thuộc đường tròn đường kính AH, hay tứ giác AFHI nội tiếp đường tròn tâm J. Do đó JF = JE (**)

Từ (*) và (**) suy ra JI là đường trung trực của đoạn thẳng EF.

Vì tứ giác BFEC nội tiếp đường tròn đường kính BC với K là trung điểm của BC, suy ra KF = KE.

Do đó, K thuộc đường trung trực của IJ của EF, hay J, I, K thẳng hàng.