Cho tam giác ABC nhọn (AB < AC) có đường cao AD và đường phân giác trong AO (D, O thuộc cạnh BC). Kẻ \(OM \bot AB\) tại M, \(ON \bot AC\) tại N.

a) Chứng minh bốn điểm O, M, D, N cùng nằm trên một đường tròn.

b) Chứng minh: \(\widehat {BDM} = \widehat {ODN}\).

c) Qua O kẻ đường thẳng vuông góc với BC cắt MN tại I, AI cắt BC tại K. Chứng minh K là trung điểm của BC.

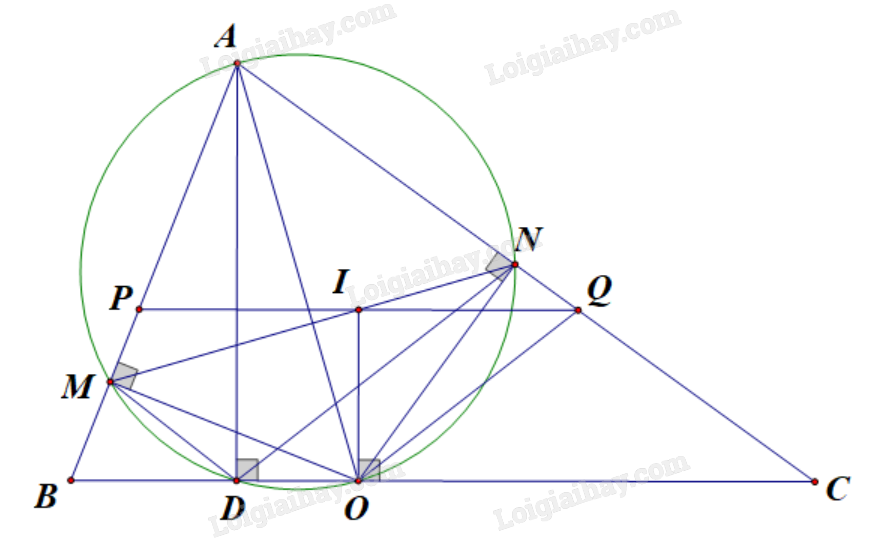
a) Ta có:

+ \(OM \bot AB\) tại M nên \(\widehat {AMO} = {90^o}\). Do đó, M thuộc đường tròn đường kính AO.

+ \(ON \bot AC\) tại N nên \(\widehat {ANO} = {90^o}\). Do đó, N thuộc đường tròn đường kính AO.

+ AD là đường cao của \(\Delta ABC\) nên \(\widehat {ADO} = {90^o}\). Do đó, D thuộc đường tròn đường kính AO.

Vậy, bốn điểm M, N, D, O cùng thuộc đường tròn đường kính AO.

b) Xét \(\Delta AMO\) và \(\Delta ANO\), có:

AO chung;

\(\widehat {AMO} = \widehat {ANO} = {90^o}\);

\(\widehat {OAM} = \widehat {OAN}\) (OA là đường phân giác trong của \(\Delta ABC\)).

Suy ra \(\Delta AMO = \Delta ANO\) (g.c.g), do đó \(\widehat {AOM} = \widehat {AON}\) (1)

Vì các điểm M, D, N cùng thuộc đường tròn đường kính AO nên ta có:

\(\widehat {AOM} = \widehat {ADM}\)(góc nội tiếp chắn cung AM) (2)

\(\widehat {AON} = \widehat {ADN}\) (góc nội tiếp chắn cung AN) (3)

Từ (1), (2) và (3) suy ra ADM = ADN.

Do đó \({90^o} - \widehat {ADM} = {90^o} - \widehat {ADN}\), suy ra \(\widehat {BDM} = \widehat {ODN}\).

c) Qua I, kẻ đường thẳng song song với BC cắt AB, AC tại P, Q.

Vì \(OI \bot BC\), mà PQ // BC nên \(OI \bot PQ\).

Ta có:

+ \(\widehat {OMP} = {90^o}\) nên M thuộc đường tròn đường kính OP.

+ Vì \(OI \bot PQ\), suy ra \(OIP = {90^o}\) nên I thuộc đường tròn đường kính OP.

Do đó OMPI là tứ giác nội tiếp, suy ra \(\widehat {POI} = \widehat {PMI}\) (góc nội tiếp chắn cung PI) (4)

Ta có:

+ \(\widehat {ONQ} = {90^o}\) nên N thuộc đường tròn đường kính OQ.

+ Vì \(OI \bot PQ\), suy ra \(\widehat {OIQ} = {90^o}\) nên I thuộc đường tròn đường kính OQ.

Do đó ONQI là tứ giác nội tiếp, suy ra \(\widehat {IOQ} + \widehat {INQ} = {180^o}\); mà \(\widehat {INQ} + \widehat {INA} = {180^o}\) (góc kề bù) nên \(\widehat {IOQ} = \widehat {INA}\) (5)

Ta có:

+ \(\widehat {INA} = \widehat {AOM}\) (góc nội tiếp chắn cung AM).

+ \(\widehat {PMI} = \widehat {AON}\) (góc nội tiếp chắn cung AN).

+ \(\widehat {AOM} = \widehat {AON}\) (chứng minh trên).

Do đó, \(\widehat {INA} = \widehat {PMI}\) (6)

Từ (4), (5) và (6) suy ra \(\widehat {POI} = \widehat {IOQ}\), do đó OI là phân giác của \(\widehat {POQ}\).

Mặt khác, \(OI \bot PQ\) nên OI vừa là đường cao, vừa là đường phân giác của \(\Delta POQ\).

Suy ra \(\Delta POQ\) cân tại O và OI cũng là đường trung tuyến của \(\Delta POQ\) nên PI = IQ.

Vì PQ // BC nên theo hệ quả của định lí Thales: \(\frac{{PI}}{{BK}} = \frac{{AI}}{{AK}} = \frac{{QI}}{{CK}}\).

Ta có \(\frac{{PI}}{{BK}} = \frac{{QI}}{{CK}}\), mà PI = QI nên BK = CK.

Vậy K là trung điểm của BC.