Đề bài

$M$ và $N$ là hai điểm trên một mặt nước phẳng lặng cách nhau một khoảng $20cm$. Tại điểm $O$ trên đường thẳng $MN$ và nằm ngoài đoạn $MN$, người ta đặt nguồn dao động theo phương vuông góc với mặt nước với phương trình $u = 5\cos \omega t\left( {cm} \right)$, tạo ra sóng trên mặt nước với bước sóng $\lambda = 15cm$. Khoảng cách xa nhất giữa hai phần tử môi trường tại $M$ và $N$ khi có sóng truyền qua là bao nhiêu?

Phương pháp giải

+ Sử dụng biểu thức tính độ lệch pha giữa hai điểm: $\Delta \varphi = \dfrac{{2\pi x}}{\lambda }$

+ Sử dụng lí thuyết về sự truyền sóng và đường tròn lượng giác

+ Biểu thức tính khoảng cách giữa 2 điểm trên phương truyền sóng: ${d^2} = \Delta {x^2} + \Delta {u^2}$

Lời giải của GV Loigiaihay.com

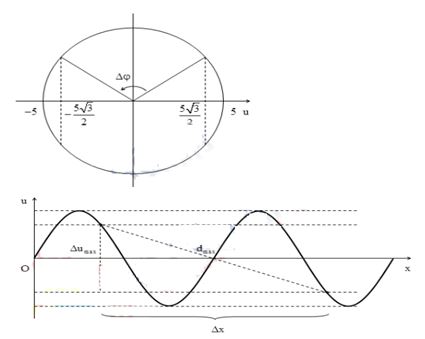
Độ lệch pha giữa hai điểm M và N: $\Delta \varphi = \dfrac{{2\pi x}}{\lambda } = \dfrac{{8\pi }}{3} = 2\pi + \dfrac{{2\pi }}{3}rad$

Khoảng cách giữa M và N là lớn nhất khi hiệu li độ giữa chúng là lớn nhất ta có $\Delta {u_{\max }} = 5\sqrt 3 cm$

Vậy khoảng cách lớn giữa M và N là ${d_{\max }} = \sqrt {\Delta {x^2} + \Delta u_{\max }^2} \approx 21,79cm$

Đáp án : D

Báo lỗi/Góp ý