Đề bài
Cổng Arch tại thành phố St.Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng m. Trên thành cổng, tại vị trí có độ cao m so với mặt đất, người ta thả một sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng một đoạn m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch.
Phương pháp giải
Chọn hệ trục tọa độ phù hợp.
Dựa vào các điểm đồ thị đi qua, thay tọa độ vào phương trình tổng quát của parabol rồi giải hệ, tìm hệ số a, b, c.
Từ đó, tìm tọa độ đỉnh của parabol và kết luận.
Lời giải của GV Loigiaihay.com
Gắn hệ toạ độ Oxy sao cho gốc toạ độ trùng với trung điểm của AB, tia AB là chiều dương của trục hoành.
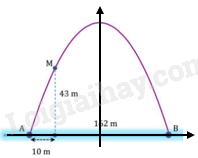
Parabol có phương trình \(y = a{x^2} + c\), đi qua các điểm: B(81;0) và M(-71;43) nên ta có hệ:
\(\left\{ \begin{array}{l}81{a^2} + c = 0\\71{a^2} + c = 43\end{array} \right. \Rightarrow c = \frac{{{{81}^2}.43}}{{{{81}^2} - 71}} \approx 185,6\)
Suy ra chiều cao của cổng là \(c \approx 185,6\) m.
