Cho đường tròn (O; R) và điểm O' khác điểm O. Với mỗi điểm M thuộc (O; R) sao cho O, O', M không thẳng hàng, vẽ hình bình hành MOO'M'. Hỏi khi M thay đổi trên (O; R) thì M' thay đổi trên đường nào?
Vẽ hình và chứng minh M’ thay đổi trên trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
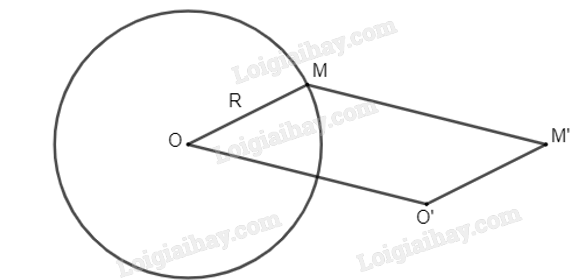
Ta có: MOO'M' là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {O'M'} \) và \(\overrightarrow {OO'} = \overrightarrow {MM'} \).
Vì OM = R nên \(O'M' = \left| {\overrightarrow {O'M'} } \right| = \left| {\overrightarrow {OM} } \right| = OM = R\) , R cố định nên O' luôn cách M' một khoảng không đổi bằng R.
Do O, O' cố định và \(\overrightarrow {OO'} = \overrightarrow {MM'} \) nên phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) biến điểm M thành điểm M'. Suy ra nếu M thay đổi trên (O; R) thì M' luôn là ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Lại có phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) biến đường tròn (O; R) thành đường tròn có bán kính là R và có tâm là ảnh của tâm O qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) hay chính là điểm O'. Điều này có nghĩa là đường tròn (O'; R) là ảnh của đường tròn (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Mà O'M' = R không đổi nên M' luôn thuộc đường tròn (O'; R).
Vậy khi M thay đổi trên (O; R) thì M' thay đổi trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).

Các bài tập cùng chuyên đề
Khi diễu hành, để đội hình được giữ vững, ở mỗi bước, những người tham gia cần tiến đều nhau về cùng một hướng. Điều này có gì liên quan tới Toán học?

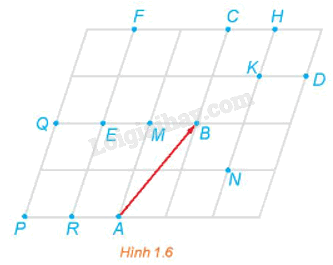
Trong Hình 1.6, tìm ảnh của các điểm M, N, P, Q, B qua phép tịnh tiến theo vectơ \(\overrightarrow {AB} \).
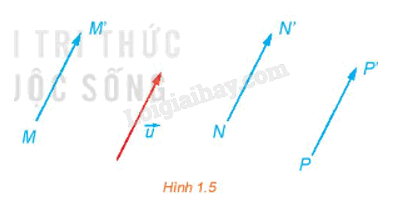
Nếu phép tịnh tiến \({T_{\overrightarrow u }}\) biến điểm M thành điểm M' thì phép tịnh tiến \({T_{ - \overrightarrow u }}\) biến điểm M' thành điểm nào?
Ở mỗi bước của đội hình diễu hành, gọi vectơ dịch chuyển của mỗi người tham gia là vectơ có điểm gốc và điểm ngọn tương ứng là vị trí trước và sau khi bước của người đó. Để giữ vững đội hình, ở mỗi bước, các vectơ dịch chuyển của những người tham gia cần có mối quan hệ gì với nhau?
Trong việc lát mặt phẳng bởi các tam giác đều bằng nhau như được thể hiện trong Hình 1.10, phép tịnh tiến theo vectơ \(\vec u\) có biến mỗi viên gạch màu xanh thành một viên gạch màu xanh, mỗi viên gạch màu đỏ thành một viên gạch màu đỏ hay không?

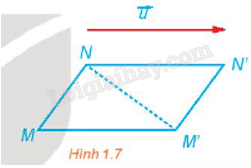
Phép tịnh tiến biến \({T_{\overrightarrow u }}\) iến M thành M', N thành N' (H.1.7).
a) Có nhận xét gì về \(\overrightarrow {MM'} + \overrightarrow {M'M} \) và \(\overrightarrow {M'N} + \overrightarrow {NN'} \).
b) Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {M'N'} \).
Cho \(\overrightarrow u \) là một vectơ chỉ phương của đường thẳng \(\Delta \). Hỏi phép tịnh tiến \({T_{\overrightarrow u }}\) biến \(\Delta \) thành đường thẳng nào?
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}1} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}2} \right)^2}\; = {\rm{ }}25\) và vectơ \(\vec u = \left( {3;\,4} \right)\).
a) Xác định ảnh của tâm đường tròn (C) qua phép tịnh tiến \({T_{\overrightarrow u }}\).
b) Viết phương trình đường tròn (C') là ảnh của (C) qua \({T_{\overrightarrow u }}\).
Trong việc lát sàn nhà như Hình 1.11, viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là ảnh của viên gạch ở góc dưới bên trái qua phép tịnh tiến theo vectơ nào? (Gợi ý: Tính vectơ tịnh tiến đó theo hai vectơ \(\overrightarrow u ,\overrightarrow v \) trên hình vẽ).

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 5 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép tịnh tiến theo vectơ \(\vec u\left( { - 3;\,4} \right)\).
Cho tam giác ABC nội tiếp đường tròn tâm O. Các đỉnh B, C cố định còn đỉnh A thay đổi trên đường tròn đó. Vẽ hình bình hành ABCD. Chứng minh rằng điểm D luôn thuộc một đường tròn cố định.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm O(0; 0) và bán kính R = 3. Xác định ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\).
Xét phép tịnh tiến theo vectơ \(\overrightarrow {MN} \) (Hình 5).
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép tịnh tiến trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.

Cho phép tịnh tiến \({T_{\vec u}}\) và hai điểm M, N. Giả sử \(M' = {T_{\vec u}}\left( M \right),\,N' = {T_{\vec u}}\left( N \right)\)
a) Biểu diễn các vectơ \(\overrightarrow {MM'} \,\) và \(\overrightarrow {NN'} \) theo \(\vec u\).
b) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow {M'N'} \) và \(\overrightarrow {MN} \).
c) So sánh các đoạn thẳng M'N' và MN.
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} .\)
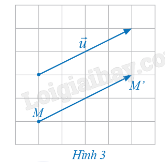
Cho vectơ \(\vec u\) và điểm M trong mặt phẳng. Hãy xác định điểm M' trong mặt phẳng sao cho \(\overrightarrow {MM'} = \vec u\) (Hình 3).
Quan sát Hình 38a và chứng minh hai hình AMPOE và CQGON bằng nhau.

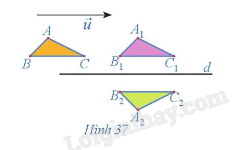
Quan sát Hình 37.
a) Chỉ ra các phép dời hình biến tam giác ABC thành tam giác A1B1C1 và biến tam giác \({A_1}{B_1}{C_1}\) thành tam giác \({A_2}{B_2}{C_2}.\)
b) Có nhận xét gì về hai tam giác ABC và \({A_2}{B_2}{C_2}?\)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm \(I\left( {--{\rm{ }}3;{\rm{ }}2} \right)\) bán kính \(R{\rm{ }} = {\rm{ }}1\). Thực hiện phép dời hình f bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\). Xác định ảnh của đường tròn (C) qua phép dời hình nói trên.
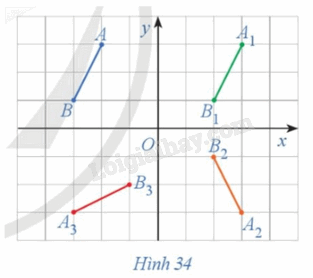
Trong Hình 34, cho đoạn thẳng AB. Nêu cách dựng:
a) Đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\);
b) Đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép đối xứng trục Ox;
c) Đoạn thẳng A3B3 là ảnh của đoạn thẳng A2B2 qua phép quay tâm O với góc quay \(\;\varphi = --90^\circ ;\)
d) So sánh độ dài các đoạn thẳng \(AB,{\rm{ }}{A_1}{B_1},{\rm{ }}{A_2}{B_2},{\rm{ }}{A_3}{B_3}.\)
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.
Cho hai đường thẳng d và d' song song với nhau.
a) Chỉ ra một phép tịnh tiến biến d thành d'.
b) Có bao nhiêu phép tịnh tiến biến d thành d'.
Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị).
Chứng minh phép đồng nhất là một phép tịnh tiến.
Trong Hình 8, người thợ sửa xe đã dùng kích nâng thủy lực để đưa ô tô từ mặt đất đến vị trí cần thiết thông qua phép biến hình nào?

Trong mặt phẳng tọa độ Oxy, xét phép tịnh tiến \({T_{\overrightarrow v }}\) với \(\overrightarrow v = (3;2).\)
a) Biết ảnh của điểm M qua \({T_{\overrightarrow v }}\) là điểm M’(–8; 5). Tìm tọa độ điểm M.
b) Tìm ảnh của đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}3} \right)^2}\; = {\rm{ }}4{\rm{ }}\)qua \({T_{\overrightarrow v }}\).
Cho vectơ \(\overrightarrow u \) và đường thẳng d. A và M là hai điểm bất kì trên d. Gọi A’ và M’ lần lượt là ảnh của A và M qua phép tịnh tiến \({{\rm{T}}_{{\rm{\vec u}}}}\).
a) Hai vectơ ‘ có bằng nhau không?
b) Khi điểm M thay đổi trên d thì điểm M’ thay đổi như thế nào? Giải thích.

Cho phép tịnh tiến \({T_{\vec v}}\) và phép tịnh tiến \({T_{\vec v}}\). Với điểm M bất kì, \({T_{\vec v}}\) biến M thành M’, \({T_{\vec v}}\) biến M’ thành M’’. Hỏi có phép tịnh tiến nào biến điểm M thành M’’ không?
Cho đường tròn (O) và hai điểm A, B. Khi điểm M thay đổi trên đường tròn (O) thì điểm M’ thay đổi trên đường nào để \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} \)?
Cho phép tịnh tiến \({T_{\vec u}}\) trong đó \(\vec u = \left( {3;5} \right)\)
a) Tìm ảnh của các điểm \(\;A\left( {-3;{\rm{ }}4} \right),{\rm{ }}B\left( {2;{\rm{ }}-7} \right)\) qua \({T_{\vec u}}\).
b) Biết rằng M’(2; 6) là ảnh của điểm M qua \({T_{\vec u}}\). Tìm tọa độ của điểm M.
c) Tìm ảnh của đường thẳng \(d:{\rm{ }}4x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}0\) qua \({T_{\vec u}}\).







Danh sách bình luận