Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(−1 ; −2), đường trung tuyến kẻ từ B và đường cao kẻ từ C lần lượt có phương trình là 5x + y – 9 = 0 và x + 3y − 5 = 0. Tìm toạ độ của hai điểm B và C.
Bước 1: Viết phương trình đường thẳng AB (có VTPT là VTCP của CH).
Bước 2: Giải hệ 2 PT BM và AB để tìm tọa độ điểm B.
Bước 3: Tham số hóa điểm M theo PT BM và biểu diễn tọa độ C theo tham số đó.
Bước 4: Thay tọa độ tham số của điểm C vào PT CH rồi tìm tọa độ điểm C.
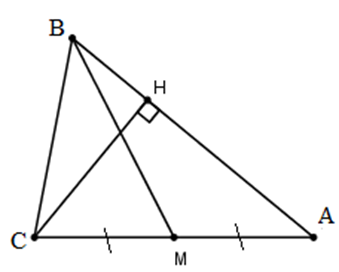
Gọi BM là đường trung tuyến kẻ từ B \( \Rightarrow BM\) có PT: 5x + y – 9 = 0.
Gọi CH là đường cao kẻ từ C \( \Rightarrow CH\) có PT: x + 3y − 5 = 0.
CH có VTPT \(\overrightarrow {{n_1}} = (1;3)\) \( \Rightarrow CH\) có VTCP \(\overrightarrow {{u_1}} = (3; - 1)\).
Ta có: \(CH \bot AB\) \( \Rightarrow AB\) đi qua A(−1 ; −2) và nhận \(\overrightarrow {{u_1}} = (3; - 1)\) làm VTPT nên có PT:
3x – y + 1 = 0.
Do B là giao điểm của BM và AB nên tọa độ điểm B là nghiệm của hệ PT:
\(\left\{ \begin{array}{l}5x + y - 9 = 0\\3x - y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 4\end{array} \right. \Rightarrow B(1;4)\).
Do \(M \in BM\) nên \(M(t;9 - 5t)\).
Theo giả thiết, M là trung điểm AC \( \Rightarrow C(2t + 1; - 10t + 20)\).
Do \(C \in CH\) nên \(2t + 1 + 3( - 10t + 20) - 5 = 0 \Leftrightarrow - 28t + 56 = 0 \Leftrightarrow t = 2\) \( \Leftrightarrow C(5;0)\).
Vậy \(B(1;4)\) và \(C(5;0)\).
Các bài tập cùng chuyên đề
Việc quy đổi nhiệt độ giữa đơn vị độ C (Anders Celsius, 1701 – 1744) và đơn vị độ F (Daniel Fahrenheit, 1 686 – 1 736) được xác định bởi hai mốc sau: Nước đóng băng ở 0°C, 32°F: Nước sôi ở 100°C, 212°F. Trong quy đổi đó, nếu a °C tương ứng với b °F thì trên mặt phẳng toạ độ Oxy, điểm M(a; b) thuộc đường thẳng đi qua A(0; 32) và B(100; 212). Hỏi 0°F, 100°F tương ứng với bao nhiêu độ C?
Theo Google Maps, sân bay Nội Bài có vĩ độ 21,2° Bắc, kinh độ 105,8° Đông, sân bay Đà Nẵng có Vĩ độ 16,1° Bắc, kinh độ 108,2° Đông. Một máy bay, bay từ Nội Bài đến sân bay Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ x° Bắc, kinh độ y° Đông được tính theo công thức
\(\left\{ \begin{array}{l}x = 21,2 - \frac{{153}}{{40}}t\\y = 105,8 + \frac{9}{5}t\end{array} \right.\)
a) Hỏi chuyển bay từ Hà Nội đến Đà Nẵng mất mấy giờ?
b) Tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến 17 ( 17 độ Bắc) chưa?
Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại ba vị trí O(0;0), A(1; 0), B(1; 3) nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh.
Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 \({m^3}/h\) vào một cái bể đã chứa sẵn 5 \({m^3}\) nước.
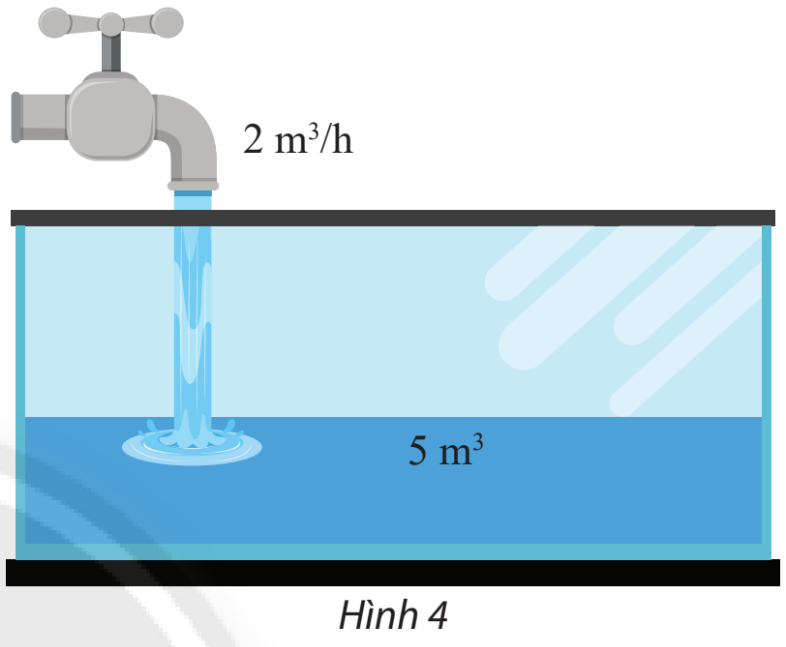
a) Viết biểu thức tính thể tích y của nước có trong bể sau x giờ.
b) Gọi \(y = f(x)\)là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số này.
c) Viết phương trình tham số và phương trình tổng quát của đường thẳng d.
Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2:
a) Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\)và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\)
Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm \(M(x;y)\) từ vị trí \(A(1;2)\) chuyển động thẳng đều với Vectơ vận tốc \(\overrightarrow v = (3; - 4)\)
a) Viết phương trình tổng quát của đường thẳng \(\Delta \) biểu diễn đường đi của điểm M.
b) Tìm tọa độ của điểm M khi \(\Delta \) cắt trục hoành.
Cho đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\).
Tìm giao điểm của d với hai trục tọa độ.
Một người đang viết chương trình cho trò chơi đá bóng robot. Gọi \(A( - 1;1),B(9;6),C(5; - 3)\)là 3 vị trí trên màn hình:
a) Viết phương trình các đường thẳng AB, AC, BC.
b) Tính góc hợp bởi hai đường thẳng AB và AC.
c) Tính khoảng cách từ điểm A đến đường thẳng BC.
Cho đường thẳng d có phương trình tham số là: \(\left\{ \begin{array}{l}x = - 1 - 3t\\y = 2 + 2t\end{array} \right.\)
a) Lập phương trình tổng quát của đường thẳng d.
b) Tìm toạ độ giao điểm của đường thẳng d lần lượt với các trục Ox, Oy.
c) Đường thẳng d có đi qua điểm M(-7; 5) hay không?
Cho đường thẳng d có phương trình tổng quát là: x - 2y – 5 = 0.
a) Lập phương trình tham số của đường thẳng d.
b) Tìm toạ độ điểm M thuộc d sao cho OM = 5 với O là gốc toạ độ.
c) Tìm toạ độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.
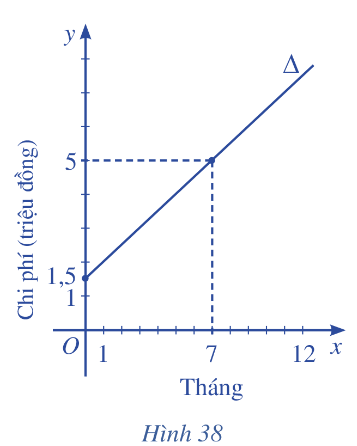
Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng \(\Delta \) ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng tập thể dục theo thời gian tập của một người (đơn vị: tháng).
a) Viết phương trình của đường thẳng \(\Delta \).
b) Giao điểm của đường thẳng \(\Delta \) với trục tung trong tình huống này có ý nghĩa gì?
c) Tính tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng.
Trong mặt phẳng toạ độ, cho đường thẳng \(\Delta \): 2x + y – 4 = 0 và điểm M(-1; 1). Gọi H là hình chiếu của M lên đường thẳng \(\Delta \).
a) Tìm một vectơ chỉ phương của đường thẳng MH.
b) Viết phương trình tham số của đường thẳng MH.
c) Tìm toạ độ của H. Từ đó, tính độ dài đoạn thẳng MH.
Trongg mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :x + 2y - 5 = 0\). Tìm mệnh đề sai trong các mệnh đề sau:
A. Vecto \(\overrightarrow n = (1;2)\) là một vecto pháp tuyến của \(\Delta \)
B. Vecto \(\overrightarrow u = ( - 2;1)\) là một vecto chỉ phương của \(\Delta \)
C. Đường thẳng \(\Delta \) song song với đường thẳng \(d:\left\{ \begin{array}{l}x = 1 - 2t\\y = 1 + t\end{array} \right.\)
D. Đường thẳng \(\Delta \)có hệ số góc \(k = 2\)
Trong mặt phẳng \(Oxy\), cho điểm \(M\left( {2;1} \right)\) và đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 - t\\y = 2t\end{array} \right.\). Tìm điểm N thuộc đường thẳng \(\Delta \) sao cho \(MN = \sqrt 2 \).
Trong mặt phẳng \(Oxy\), cho hình vuông ABCD có \(A\left( { - 1;0} \right)\) và \(B\left( {1;2} \right)\).
a) Lập phương trình đường thẳng BC.
b) Tìm tọa độ của điểm C biết rằng hoành hộ của điểm C là số dương.
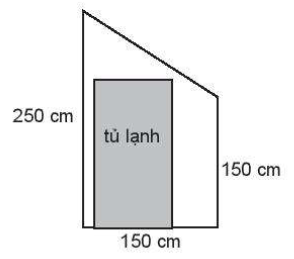
Nhà bạn Nam định đổi tủ lạnh và dự định kê vào vị trí dưới cầu thang. Biết vị trí kê tủ lạnh có mặt cát là một hình thang vuông với hai đáy lần lượt là 150 cm và 250 cm, chiều cao là 150 cm (như hình vẽ). Bố mẹ Nam định mua một tủ lạnh 2 cánh (Slide by slide) có chiều cao là 183 cm và bề ngang 90 cm. Bằng cách sử dụng tọa độ trong mặt phẳng, em hãy giúp Nam tính xem bố mẹ Nam có thể kê vừa chiếc tủ lạnh vào vị trí cần kê không?
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 4 + t\\y = - 1 + 2t\end{array} \right.\) và điểm A(2 ; 1). Hai điểm M, N nằm trên ∆.
a) Tìm toạ độ điểm M sao cho AM = \(\sqrt {17} \).
b) Tìm toạ độ điểm N sao cho đoạn thẳng AN ngắn nhất.
Cho ba điểm A(-2 ; 2), B(7 ; 5), C(4 ; – 5) và đường thẳng ∆: 2x + y – 4 = 0.
a) Tìm toạ độ điểm M thuộc ∆ và cách đều hai điểm A và B.
b*) Tìm toạ độ điểm N thuộc ∆ sao cho |\(\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} \)| có giá trị nhỏ nhất.
