Cho tam giác ABC vuông tại A có AB < AC, đường phân giác BD. Vẽ DE vuông góc với BC tại E.
a) Chứng minh trực tâm H của tam giác BAE nằm trên đường thẳng BD.
b) Chứng minh trực tâm của tam giác DAE nằm ngoài tam giác đó.
c) Tìm điều kiện của tam giác ABC để H cách đều các đỉnh của tam giác BAE.
- Chứng minh: BK là đường cao của tam giác BAE và B, K, D thẳng hàng nên trực tâm H của tam giác BAE nằm trên đường thẳng BD.
- Chứng minh: \(\widehat {ADE} > 90^\circ \) nên suy ra trực tâm của tam giác DAE nằm ngoài tam giác đó.
- Tam giác ABE có H là trực tâm, để H cách đều các đỉnh của tam giác BAE thì tam giác BAE là tam giác đều từ đó suy ra điều kiện của tam giác ABC.
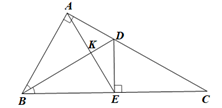
a) Gọi K là giao điểm của BD và AE.
Xét ∆BAD và ∆BED có:
\(\widehat {BAD} = \widehat {BED}\left( { = 90^\circ } \right)\)
BD là cạnh chung,
\(\widehat {ABD} = \widehat {EBD}\) (do BD là tia phân giác của góc ABC)
Do đó ∆BAD = ∆BED (cạnh huyền – góc nhọn).
Suy ra BA = BE (hai cạnh tương ứng).
Xét DABK và DEBK có:
BA = BE (chứng minh trên),
\(\widehat {ABK} = \widehat {EBK}\) (do BD là tia phân giác của góc ABC),
BK là cạnh chung
Do đó DABK =DEBK (c.g.c)
Suy ra \(\widehat {BKA} = \widehat {BKE}\) (hai góc tương ứng).
Mà \(\widehat {BKA} + \widehat {BKE} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {BKA} = \widehat {BKE} = \frac{{180^\circ }}{2} = 90^\circ \)
Hay BK ⊥ AE.
Do BK là đường cao của tam giác BAE và B, K, D thẳng hàng nên trực tâm H của tam giác BAE nằm trên đường thẳng BD.
Vậy trực tâm H của tam giác BAE nằm trên đường thẳng BD.
b)Ta có \(\widehat {ADE} + \widehat {EDC} = 180^\circ \) (hai góc kề bù)
Mà \(\widehat {EDC} < 90^\circ \) (vì tam giác ECD vuông tại E nên góc EDC là góc nhọn)
Suy ra \(\widehat {ADE} > 90^\circ \)
Do góc ADE là góc tù nên trực tâm của tam giác DAE nằm ngoài tam giác đó.
Vậy trực tâm của tam giác DAE nằm ngoài tam giác đó.
c) Xét tam giác ABE có H là trực tâm, để H cách đều các đỉnh của tam giác BAE thì tam giác BAE là tam giác đều
Do đó \(\widehat {ABE} = 60^\circ \) hay \(\widehat {ABC} = 60^\circ \) Vậy điều kiện để H cách đều các đỉnh của tam giác BAE là tam giác ABC vuông tại A có \(\widehat {ABC} = 60^\circ \).

Các bài tập cùng chuyên đề
Vẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không ?
a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB.
Cho tam giác ABC có \(\widehat A = {100^0}\) và trực tâm H. Tìm góc BHC.
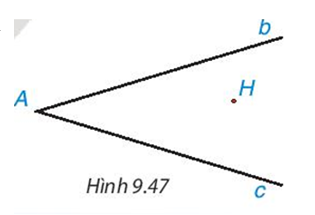
Cho hai đường thẳng không vuông góc b,c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.47). Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.
Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.
Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC
b) BE vuông góc với DC
Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.
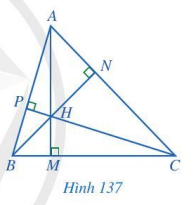
Quan sát ba đường cao AM, BN, CP của tam giác ABC (Hình 137), cho biết ba đường cao đó có cùng đi qua một điểm hay không.
Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.
Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.
Cho tam giác ABC có H là trực tâm, H không trùng với đỉnh nào của tam giác. Nêu một tính chất của cặp đường thẳng:
a) AH và BC; b) BH và CA; c) CH và AB.
Cho tam giác ABC. Vẽ trực tâm H của tam giác ABC và nhận xét vị trí của nó trong các trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
Cho tam giác nhọn ABC và điểm D nằm trong tam giác. Chứng minh rằng nếu DA vuông góc với BC và DB vuông góc CA thì DC vuông góc với AB.
Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, \(\widehat {HCA} = 25^\circ \). Tính \(\widehat {BAC}\) và \(\widehat {HBA}\).
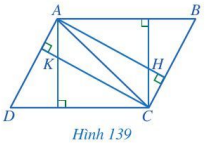
Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD. Chứng minh AK // CH và AH // CK.
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:
a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;
b) Nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
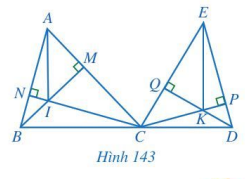
Cho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng hàng. Hai đường cao BM và CN của tam giác ABC cắt nhau tại I, hai đường cao CP và DQ của tam giác ECD cắt nhau tại K (Hình 143). Chứng minh AI // EK.
Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 145). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ D đến điểm A là nhỏ nhất? Em hãy giúp bạn Hùng tìm cách vẽ điểm D và giải thích cách làm của mình?
Cho tam giác ABC vuông. Kẻ đường thẳng vuông góc với cạnh huyền BC của tam giác ABC tại điểm D không thuộc đoạn BC. Nó cắt đường thẳng chứa cạnh AB tại E và cắt đường thẳng chứa cạnh AC tại F. Xác định trực tâm của tam giác BEF.
Trong hình 7. Hãy chứng minh AC, EK và BD cùng đi qua một điểm.

Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Vẽ hai đường cao AE và AF của hai tam giác Abc và ACD. Chứng minh góc EAF vuông.
Cho tam giác ABC có \(\widehat {{A^{}}} = {65^o},\widehat B = {54^o}\). Vẽ trực tâm H của tam giác ABC, Tính góc AHB.
Cho tam giác ABC cân tại A có góc A nhọn và H là trực tâm. Cho biết \(\widehat {BHC} = {150^o}\). Tính các góc của tam giác ABC.







Danh sách bình luận