Tìm số đo góc giữa hai đường thẳng của mỗi cặp đường thẳng sau:
a) ∆1: 3x + y - 5 = 0 và ∆2: x + 2y − 3 = 0.
b) \({\Delta _3}:\left\{ \begin{array}{l}x = 2 + \sqrt 3 t\\y = - 1 + 3t\end{array} \right.\) và \({\Delta _4}:\left\{ \begin{array}{l}x = 3 - \sqrt 3 t'\\y = - t'\end{array} \right.\).
c) \({\Delta _5}: - \sqrt 3 x + 3y + 2 = 0\) và \({\Delta _6}:\left\{ \begin{array}{l}x = 3t\\y = 1 - \sqrt 3 t\end{array} \right.\).
Bước 1: Đưa các PT của mỗi ý về cùng dạng PT đường thẳng.
Bước 2: Tính góc giữa hai vectơ pháp tuyến (chỉ phương) của 2 đường thẳng rồi suy ra góc giữa hai đường thẳng tương ứng.
a) ∆1: 3x + y - 5 = 0 và ∆2: x + 2y − 3 = 0.
∆1 có VTPT là \(\overrightarrow {{n_1}} = (3;1)\); ∆2 có VTPT là \(\overrightarrow {{n_2}} = (1;2)\).
Ta có: \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{3.1 + 1.2}}{{\sqrt {{3^2} + {1^2}} .\sqrt {{1^2} + {2^2}} }}\)\( = \frac{{\sqrt 2 }}{2}\)\( \Rightarrow \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = {45^0}\).
Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {45^0}\).
b) \({\Delta _3}:\left\{ \begin{array}{l}x = 2 + \sqrt 3 t\\y = - 1 + 3t\end{array} \right.\) và \({\Delta _4}:\left\{ \begin{array}{l}x = 3 - \sqrt 3 t'\\y = - t'\end{array} \right.\).
∆3 có VTCP là \(\overrightarrow {{u_1}} = (\sqrt 3 ;3)\); ∆4 có VTPT là \(\overrightarrow {{u_2}} = ( - \sqrt 3 ; - 1)\).
Ta có: \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \frac{{\sqrt 3 .\left( { - \sqrt 3 } \right) + 3.( - 1)}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {3^2}} .\sqrt {{{\left( { - \sqrt 3 } \right)}^2} + {{( - 1)}^2}} }}\)\( = - \frac{{\sqrt 3 }}{2}\)\( \Rightarrow \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = {150^0}\).
Vậy \(\left( {{\Delta _3},{\Delta _4}} \right) = {180^0} - {150^0} = {30^0}\).
c) \({\Delta _5}: - \sqrt 3 x + 3y + 2 = 0\) và \({\Delta _6}:\left\{ \begin{array}{l}x = 3t\\y = 1 - \sqrt 3 t\end{array} \right.\).
∆5 có VTPT là \(\overrightarrow n = ( - \sqrt 3 ;3)\) \( \Rightarrow {\Delta _5}\) có một VTCP là \(\overrightarrow {{u_3}} = (3;\sqrt 3 )\).
∆6 có VTCP là \(\overrightarrow {{u_4}} = (3; - \sqrt 3 )\).
Ta có: \(\cos \left( {\overrightarrow {{u_3}} ,\overrightarrow {{u_4}} } \right) = \frac{{3.3 + \sqrt 3 .\left( { - \sqrt 3 } \right)}}{{\sqrt {{3^2} + {{\left( {\sqrt 3 } \right)}^2}} .\sqrt {{3^2} + {{\left( { - \sqrt 3 } \right)}^2}} }}\)\( = \frac{1}{2}\)\( \Rightarrow \left( {\overrightarrow {{u_3}} ,\overrightarrow {{u_4}} } \right) = {60^0}\).
Vậy \(\left( {{\Delta _5},{\Delta _6}} \right) = {60^0}\).
Các bài tập cùng chuyên đề
Tính góc giữa hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 2 + t\\y = 1 - 2t\end{array} \right.,{\rm{ }}{\Delta _2}:\left\{ \begin{array}{l}x = 1 + t'\\y = 5 + 3t'\end{array} \right.\)
Hai đường thẳng cắt nhau \({\Delta _1},{\Delta _2}\) tương ứng có các vecto pháp tuyến \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \). Gọi \(\varphi \) là góc giữa hai đường thẳng đó. Nêu mối quan hệ giữa:
a) \(\varphi \) và góc \(\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\).
b) \(\cos \varphi \) và \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\).
Tính góc giữa hai đường thẳng: \({\rm{ }}{\Delta _1}:{\rm{ }}x + 3y + 2{\rm{ }} = {\rm{ }}0,{\rm{ }}{\Delta _2}:{\rm{ }}y = 3x + 1\)
Tính góc giữa hai đường thẳng:
a) \({\Delta _1}:\sqrt 3 x + y - 4 = 0\) và\({\Delta _2}:x + \sqrt 3 y + 3 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = - 1 + 2t\\y = 3 + 4t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 3 + s\\y = 1 - 3s\end{array} \right.\)
Tìm số đo của góc giữa hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) trong các trường hợp sau:
a) \({\Delta _1}:x + 3y - 7 = 0\) và \({\Delta _2}:x - 2y + 3 = 0\).
b) \({\Delta _1}:4x - 2y + 5 = 0\) và \({\Delta _2}:\left\{ \begin{array}{l}x = t\\y = 13 + 2t\end{array} \right.\)
c) \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 3 + 2t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 7 + 2t\\y = 1 - t\end{array} \right.\)
Tìm số đo của góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:x - 2y + 3 = 0\) và \({d_2}:3x - y - 11 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = t\\y = 3 + 5t\end{array} \right.\) và \({d_2}:x + 5y - 5 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 3 + 2t\\y = 7 + 4t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = t\\y = - 9 + 2t\end{array} \right.\)
Tìm tọa độ giao điểm và góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) trong mỗi trường hợp sau:
a) \({d_1}:x - y + 2 = 0\) và \({d_2}:x + y + 4 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = 1 + t\\y = 3 + 2t\end{array} \right.\) và \({d_2}:x - 3y + 2 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 1 + 3t'\\y = 3 + t'\end{array} \right.\)
Tính số đo góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong môi trường hợp sau:
a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 3 + 3\sqrt 3 t\\y = 2 + 3t\end{array} \right.\) và \({\Delta _2}:y - 4 = 0\).
b) \({\Delta _1}:2x - y = 0\) và \({\Delta _2}: - x + 3y - 5 = 0\).
Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} = {\rm{ }}\left( {{a_1};{\rm{ }}{b_1}} \right),{\rm{ }}\overrightarrow {{u_2}} {\rm{ }} = {\rm{ }}\left( {{a_2};{b_2}} \right)\) . Tính \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\).
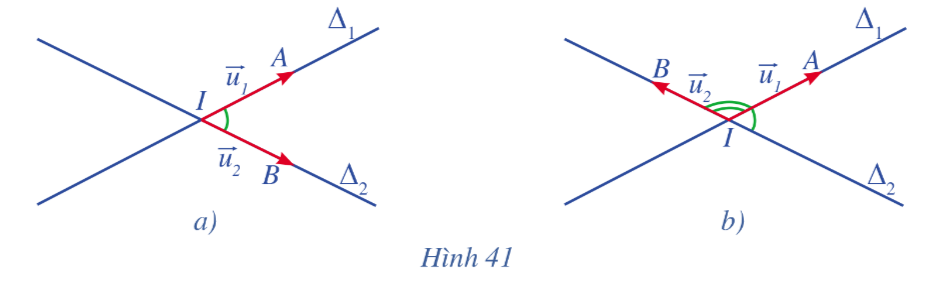
Cho hai đường thẳng \({\Delta _1},{\Delta _2}\) cắt nhau tại I và có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Gọi A và B là các điểm lần lượt thuộc hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) sao cho \(\overrightarrow {{u_1}} = \overrightarrow {IA} ,\overrightarrow {{u_2}} = \overrightarrow {IB} \).
a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng.
\({\Delta _1},{\Delta _2}\)và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \),\(\overrightarrow {IB} \).
b) Chứng tỏ cos(\({\Delta _1},{\Delta _2}\)) = \(\left| {cos\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\).
Tính số đo góc giữa hai đường thẳng \({d_1}:2x - y + 5 = 0\) và\({d_2}:x - 3y + 3 = 0\).
Tính góc giữa các cặp đường thẳng sau:
a) \(d:y - 1 = 0\) và \(k:x - y + 4 = 0\).
b) \(a:\left\{ \begin{array}{l}x = 3 + t\\y = 2t\end{array} \right.\) và \(b:3x + y + 1 = 0\).
c) \(m:\left\{ \begin{array}{l}x = 1 - t\\y = 2 - \sqrt 3 t\end{array} \right.\) và \(n:\left\{ \begin{array}{l}x = 4 - t'\\y = \sqrt 3 t'\end{array} \right.\).
Cho hai đường thẳng \(d:x - 2y - 5 = 0\) và \(k:x + 3y + 3 = 0\). Góc giữa hai đường thẳng d và k là:
A. \({30^ \circ }\)
B. \({135^ \circ }\)
C. \({45^ \circ }\)
D. \({60^ \circ }\)
Tìm số đo của góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:5x - 3y + 1 = 0\) và \({d_2}:10x - 6y - 7 = 0\).
b) \({d_1}:7x - 3y + 7 = 0\) và \({d_2}:3x + 7y - 10 = 0\).
c) \({d_1}:2x - 4y + 9 = 0\) và \({d_2}:6x - 2y - 2023 = 0\).
Tìm góc giữa hai đường thẳng \({d_1}\) và \({d_2}\).
a) \({d_1}:5x - 9y + 2019 = 0\) và \({d_2}:9x + 5y + 2020 = 0\).
b) \({d_1}:\left\{ \begin{array}{l}x = 9 + 9t\\y = 7 + 18t\end{array} \right.\) và \({d_2}:4x - 12y + 13 = 0\).
c) \({d_1}:\left\{ \begin{array}{l}x = 11 - 5t\\y = 13 + 9t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 13 + 10t\\y = 11 - 18t\end{array} \right.\).
Cho ∆1: x − 2y + 3 = 0 và ∆2: -2x – y + 5 = 0. Số đo góc giữa hai đường thẳng ∆1 và ∆2 là:
A. 30⁰
B. 45⁰
C. 90°
D. 60⁰
Cho \({\Delta _1}:\left\{ \begin{array}{l}x = - 2 + \sqrt 3 t\\y = 1 - t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 1 + \sqrt 3 t'\\y = 2 + t'\end{array} \right.\). Số đo góc giữa hai đường thẳng ∆1 và ∆2 là:
A. 300
B. 450
C. 900
D. 600
Trong mặt phẳng toạ độ Oxy, cho hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 2 + \sqrt 3 t\\y = - 1 + 3t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 3 - \sqrt 3 t'\\y = - t'\end{array} \right.\)
Số đo góc giữa hai đường thẳng ∆1 và ∆2 là:
A. 300
B. 450
C. 900
D. 600
A. \(\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
B. \(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
C. \(\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} + \sqrt {a_2^2 + b_2^2} }}\).
D. \(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} + \sqrt {a_2^2 + b_2^2} }}\).
A. \(45^\circ \)
B. \(60^\circ \)
C. \(90^\circ \)
D. \(30^\circ \)
Có hai con tàu A, B xuất phát từ hai bến, chuyển động theo đường thẳng ngoài biển. Trên màn hình ra-đa của trạm điều khiển (xem như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính bằng ki-lô-met), tại thời điểm t (giờ), vị trí của tàu A có tọa độ được xác định bởi công thức $\begin{cases} x = 3 - 33t \\ y = -4 + 25t \end{cases}$; vị trí tàu B có tọa độ là (4 - 30t; 3 - 40t). Giả sử a là côsin góc giữa hai đường đi của hai tàu A, B. Tính 100a (làm tròn kết quả đến hàng phần trăm).
Một chiếc Phà chở khách qua sông từ điểm A(3; 4) đến điểm B(3; 50) bên kia sông. Nhưng vì có gió và nước chảy mạnh nên chiếc Phà qua bên kia sông tại điểm C(38; 50). Góc lệch của con thuyền với lúc dự tính ban đầu là bao nhiêu độ? Kết quả làm tròn đến hàng đơn vị.
Danh sách bình luận