Cho tam giác ABC cân tại A, vẽ đường trung tuyến AM. Qua A vẽ đường thẳng d vuông góc với AM. Chứng minh d // BC.
Chứng minh d và BC cùng vuông góc với AM.
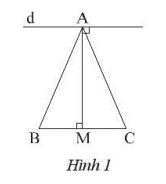
Ta có: \(\Delta AMB = \Delta AMC\) (c – c – c) vì cạnh AM chung, AB = AC (tam giác ABC cân tại A), MB = MC (AM là đường trung tuyến)
Suy ra: \(\widehat {AMB} = \widehat {AMC} = \frac{{{{180}^o}}}{2} = {90^o}\)
Ta có d và BC cùng vuông góc với AM suy ra d // BC.
Các bài tập cùng chuyên đề
Mỗi tam giác có mấy đường cao?
Em hãy dựng tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh AC của tam giác.
Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC
Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a)
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b
Cho tam giác ABC. Gọi M, N, P lần lượt là hình chiếu của A, B, C trên các đường thẳng BC, CA, AB (Hình 132).
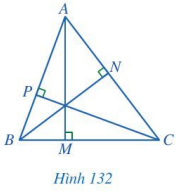
Em có nhận xét gì về ba đường thẳng AM, BN, CP?
Cho tam giác ABC ( Hình 133). Bằng cách sử dụng ê ke, vẽ hình chiếu M của điểm A trên đường thẳng BC.
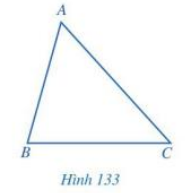
Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C.
