Cho hình chữ nhật MNPQ và ngũ giác ABCDE trên lưới ô vuông như Hình 8, với cạnh của mỗi ô vuông nhỏ là 1 cm. Tính tỉ số diện tích ngũ giác ABCDE và diện tích hình chữ nhật MNPQ (làm tròn đến hàng phần mười).
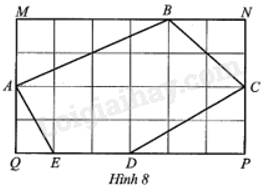
Tính các diện tính tam giác ABM, CBN, CPD, AQE. Sau đó tính diện tích hình chữ nhật MNPQ. Từ đó suy ra diện tích ngũ giác bằng hiệu diện tích hình chữ nhật MNPQ và tổng diện tích các tam giác.
Diện tích của tam giác ABM là: \(\frac{1}{2}.4.2 = 4\) (cm2)
Diện tích của tam giác CBN là: \(\frac{1}{2}.2.2 = 2\)(cm2)
Diện tích của tam giác CPD là: \(\frac{1}{2}.3.2 = 3\)(cm2)
Diện tích của tam giác AQE là: \(\frac{1}{2}.1.2 = 1\)(cm2)
Tổng diện tích các tam giác ABM, CBN, C PD, AQE là:
4 + 2 + 3 + 1 = 10 (đơn vị diện tích).
Diện tích hình chữ nhật MNPQ là: 6.4 = 24 (đơn vị diện tích).
Diện tích ngũ giác ABCDE là hiệu diện tích hình chữ nhật MNPQ và tổng diện tích các tam giác ABM, CBN, C PD, AQE, và bằng:
24 – 10 = 14 (đơn vị diện tích).
Tỉ số diện tích ngũ giác ABCDE và diện tích hình chữ nhật MNPQ là: \(\frac{{14}}{{24}} = \frac{7}{{12}} \approx 0,6.\)

Các bài tập cùng chuyên đề
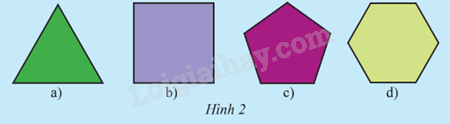
Có nhận xét gì về các cạnh và góc của mỗi đa giác sau?
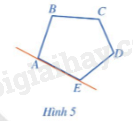
Nêu đặc điểm về vị trí của ngũ giác ABCDE so với đường thẳng chứa một cạnh bất kì của ngũ giác đó (Hình 5)
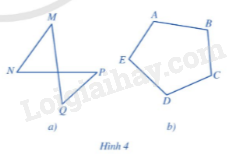
Tứ giác MNPQ ở Hình 4a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM. Ngũ giác ABCDE gồm 5 đỉnh A, B, C, D, E và 5 cạnh AB, BC, CD, DE, EA. Quan sát hai hình đó, hãy cho biết các phát biểu sau là đúng hay sai:
a) Mỗi đỉnh là điểm chung của đúng hai cạnh.
b) Không có hai cạnh nào nằm trên cùng một đường thẳng.
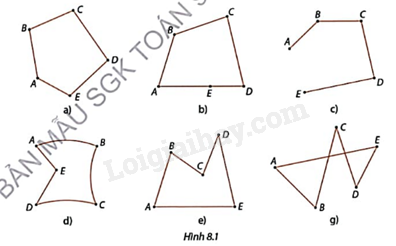
Trong Hình 8.1, hãy cho biết những hình nào có tính chất:
Tạo bởi các đoạn thẳng AB, BC, CD, DE, EA;
Bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
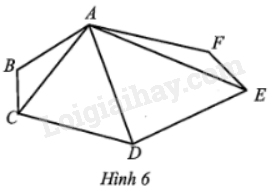
Quan sát Hình 6 và kể tên các đa giác có trong hình đó.
Cho ngũ giác ABCDE. Chứng minh:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.







Danh sách bình luận