Viết phương trình chính tắc của:
a) Elip có trục lớn bằng 12 và trục nhỏ bằng 8.
b) Hypebol có tiêu cự \(2c = 18\) và độ dài trục thực \(2a = 14\).
c) Parabol có tiêu điểm \(F\left( {5;0} \right)\).
Phương trình Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\)và có tiêu cự là \(2c\) với \(c = \sqrt {{a^2} - {b^2}} \).
Phương trình Hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\)và có tiêu cự là \(2c\) với \(c = \sqrt {{a^2} + {b^2}} \).
Parabol \(\left( P \right)\) có dạng \({y^2} = 2px\) với \(p > 0\) có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\).
a) Trục lớn 2a = 12, trục nhỏ 8 = 2b.
\( \Rightarrow \left\{ \begin{array}{l}a = 6\\b = 4\end{array} \right. \Rightarrow PTCT:\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\)
b) Tiêu cự \(2c = 18 \Rightarrow c = 9\), trục thực \(2a = 14 \Rightarrow a = 7\).
\(c = \sqrt {{a^2} + {b^2}} \Rightarrow {b^2} = {c^2} - {a^2} = 32 \Rightarrow \frac{{{x^2}}}{{49}} - \frac{{{y^2}}}{{32}} = 1\).
c) Parabol có tiêu điểm \(F\left( {5;0} \right) = \left( {\frac{p}{2};0} \right) \Rightarrow p = 10 \Rightarrow {y^2} = 20x\).

Các bài tập cùng chuyên đề
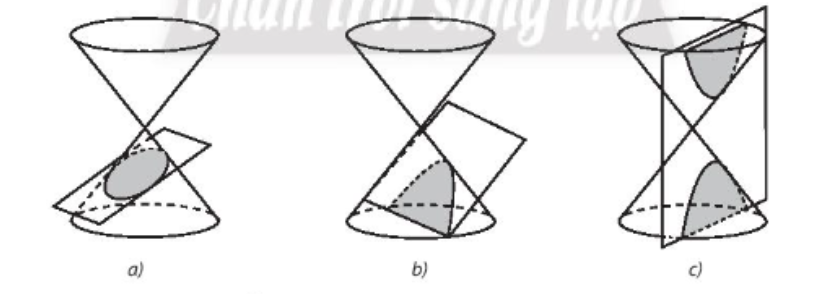
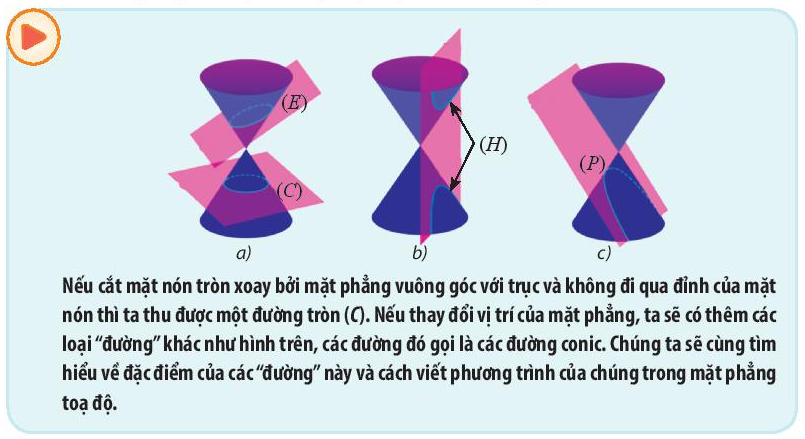
Nếu cắt mặt nón tròn xoay bởi mặt phẳng vuông góc với trục và không đi qua đỉnh của mặt nón thì ta thu được một đường tròn (C). Nếu thay đổi vị trí của mặt phẳng, ta sẽ có thêm các loại “đường” khác như hình trên, các đường đó gọi là các đường conic. Chúng ta sẽ cùng tìm hiểu về đặc điểm của các “đường” này và cách viết phương trình của chúng trong mặt phẳng tọa độ.
Viết phương trình chính tắc của:
a) Elip có trục lớn bằng 20 và trục nhỏ bằng 16.
b) Hypebol có tiêu cự \(2c = 20\) và độ dài trục thực \(2a = 12\).
c) Parabol có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\).
Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ của các tiêu điểm của chúng.
a) \(({C_1}):4{x^2} + 16{y^2} = 1\)
b) \(({C_2}):16{x^2} - 4{y^2} = 144\)
c) \(({C_3}):x = \frac{1}{8}{y^2}\)
Từ xa xưa, người Hy Lạp đã biết rằng giao tuyến của mặt nón tròn xoay và một mặt phẳng không đi qua đỉnh của mặt nón là đường tròn hoặc đường cong mà ta gọi là đường conic (Hình 48). Từ “đường conic” xuất phát từ góc tiếng Hy Lạp konos, nghĩa là mặt nón.
Đường conic gồm những loại đường nào và được xác định như thế nào?
Để lập phương trình của đường hypebol trong mặt phẳng, trước tiên ta sẽ chọn hệ trục toạ độ Oxy thuận tiện nhất. Tương tự elip, ta chọn trục Ox là đường thẳng \({F_1}{F_2}\), trục Oy là đường trung trực của đoạn thẳng \({F_1}{F_2} = {\rm{ }}2c{\rm{ }}\left( {c{\rm{ }} > {\rm{ }}0} \right)\), gốc toạ độ O là trung điểm của đoạn thẳng \({F_1}{F_2}\) (Hình 54).
a) Tìm toạ độ của hai tiêu điểm \({F_1},{F_2}\).
b) Nếu dự đoán thích hợp cho “?” trong bảng sau:

Cho biết mỗi đường conic có phương trình dưới đây là đường conic dạng nào (elip, hypebol, parabol) và tìm tọa độ tiêu điểm của đường conic đó.
a) \({y^2} = 18x\)
b) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\)
c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
Các phương trình dưới đây là phương trình chính tắc của đường nào? Khi đó hãy tìm các tiêu điểm, tiêu cực, đường chuẩn (nếu là đường parabol).
a) \({y^2} = 10x\).
b) \({x^2} - {y^2} = 1\).
c) \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ các tiêu điểm của chúng.
a) \(\left( {{C_1}} \right):7{x^2} + 13{y^2} = 1\).
b) \(\left( {{C_2}} \right):25{x^2} - 9{y^2} = 225\).
c) \(\left( {{C_3}} \right):x = 2{y^2}\).
Gọi tên các đường conic sau:
Trong mặt phẳng toạ độ Oxy, cho hai điểm F1(−4 ; 0) và F2(4 ; 0).
a) Lập phương trình đường tròn có đường kính là F1F2.
b) Tập hợp các điểm M trong mặt phẳng toạ độ thoả mãn MF1 + MF2 = 12 là một đường conic (E). Cho biết (E) là đường conic nào và viết phương trình chính tắc của (E).
c) Tập hợp các điểm M trong mặt phẳng toạ độ thoả mãn |MF1 – MF2| = 4 là một đường conic (H). Cho biết (H) là đường conic nào và viết phương trình chính tắc của (H).







Danh sách bình luận