Cho biểu thức \(P = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\) với \(x \ne \pm 1\).
a) Rút gọn P.
b) Tính giá trị của P khi \(x = 2\).
a) Thực hiện quy đồng mẫu để rút gọn P.
b) Kiểm tra xem \(x = 2\) có thỏa mãn điều kiện hay không.
Thay \(x = 2\) vào P để tính giá trị.
a) Ta có:
\(\begin{array}{l}P = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\\ = \frac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \frac{{3\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \frac{{6x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} + x + 3x - 3 - 6x + 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} + \left( {x + 3x - 6x} \right) + \left( { - 3 + 4} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} - 2x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{x - 1}}{{x + 1}}\end{array}\)
b) Ta thấy \(x = 2\) thỏa mãn điều kiện \(x \ne \pm 1\) của P.
Thay \(x = 2\) vào biểu thức P, ta được:
\(P = \frac{{2 - 1}}{{2 + 1}} = \frac{1}{3}\)
Vậy với \(x = 2\) thì \(P = \frac{1}{3}\).

Các bài tập cùng chuyên đề
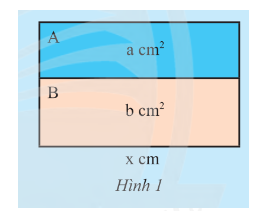
Một hình chữ nhật lớn được ghép bởi hai hình chữ nhật A và B lần lượt có diện tích là \(a\) \(c{m^2}\) và có cùng chiều dài \(x\) cm (Hình 1).
a) Tính chiều rộng của hình chữ nhật lớn theo hai cách khác nhau.
b) Chiều rộng của B lớn hơn chiều rộng của A bao nhiêu? Biết \(b > a\)
Thực hiện các phép tính cộng, trừ phân thức sau:
a) \(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\) b) \(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\) c) \(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\)
Cho hai phân thức \(A = \dfrac{{a + b}}{{ab}}\) và \(B = \dfrac{{a - b}}{{{a^2}}}\)
a) Tìm đa thức thích hợp thay vào mỗi sau đây:
\(\dfrac{{a + b}}{{ab}}\);
\(\dfrac{{a - b}}{{{a^2}}}\)
b) Sử dụng kết quả trên, tính \(A + B\) và \(A - B\)
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\dfrac{a}{{a - 3}} - \dfrac{3}{{a + 3}}\)
b) \(\dfrac{1}{{2x}} + \dfrac{2}{{{x^2}}}\)
c) \(\dfrac{4}{{{x^2} - 1}} - \dfrac{2}{{{x^2} + x}}\)
Thực hiện phép tính: \(\dfrac{x}{{x + y}} + \dfrac{{2xy}}{{{x^2} - {y^2}}} - \dfrac{y}{{x + y}}\)
Viết biểu thức tính tổng thời gian đi và về, chênh lệch thời gian giữa đi và về của đội đua thuyền ở tình huống trong câu hỏi mở đầu (trang 31). Tính giá trị của các đại lượng này khi \(x = 6\)km/h.

Thực hiện các phép cộng, trừ phân thức sau:
a) \(\dfrac{{a - 1}}{{a + 1}} + \dfrac{{3 - a}}{{a + 1}}\) b) \(\dfrac{b}{{a - b}} + \dfrac{a}{{b - a}}\) c) \(\dfrac{{{{\left( {a + b} \right)}^2}}}{{ab}} - \dfrac{{{{\left( {a - b} \right)}^2}}}{{ab}}\)
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\dfrac{1}{{2a}} + \dfrac{2}{{3b}}\)
b) \(\dfrac{{x - 1}}{{x + 1}} - \dfrac{{x + 1}}{{x - 1}}\)
c) \(\dfrac{{x + y}}{{xy}} - \dfrac{{y + z}}{{yz}}\)
d) \(\dfrac{2}{{x - 3}} - \dfrac{{12}}{{{x^2} - 9}}\)
e) \(\dfrac{1}{{x - 2}} + \dfrac{2}{{{x^2} - 4x + 4}}\)
Thực hiện các phép tính sau:
a) \(\dfrac{{x + 2}}{{x - 1}} - \dfrac{{x - 3}}{{x - 1}} + \dfrac{{x - 4}}{{1 - x}}\)
b) \(\dfrac{1}{{x + 5}} - \dfrac{1}{{x - 5}} + \dfrac{{2x}}{{{x^2} - 25}}\)
c) \(x + \dfrac{{2{y^2}}}{{x + y}} - y\)
Cùng đi từ thành phố A đến thành phố B cách nhau \(450\)km, xe khách chạy với tốc độ \(x\) (km/h); xe tải chạy với tốc độ \(y\) (km/h) (\(x > y\)). Nếu xuất phát cùng lúc thì xe khách đến thành phố B sớm hơn xe tải bao nhiêu giờ?
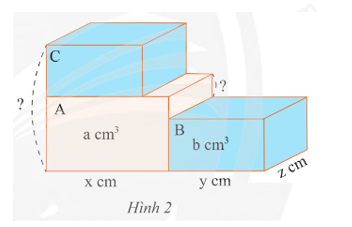
Có ba hình hộp chữ nhật A, B, C có chiều dài, chiều rộng và thể tích được cho như hình 2. Hình B và C có các kích thước giống nhau, hình A có cùng chiều rộng với B và C.
a) Tính chiều cao của các hình hộp chữ nhật. Biểu thị chúng bằng các phân thức cùng mẫu số.
b) Tính tổng chiều cao của hình A và C, chênh lệch chiều cao của hình A và B.
Tâm đạp xe từ nhà tới câu lạc bộ câu cá có quãng đường dài \(15\)km với tốc độ \(x\)(km/h). Lượt về thuận chiều gió nên tốc độ nhanh hơn lượt đi \(4\)km/h.
a) Viết biểu thức biểu thị tổng thời gian \(T\) hai lượt đi và về.
b) Viết biểu thức biểu thị hiệu thời gian \(t\) luợt đi đối với lượt về.
c) Tính \(T\) và \(t\) với \(x = 10\)
Thực hiện các phép tính sau:
a) \(\dfrac{{2{x^2} - 1}}{{x - 2}} + \dfrac{{ - {x^2} - 3}}{{x - 2}}\)
b) \(\dfrac{x}{{x + y}} + \dfrac{y}{{x - y}}\)
c) \(\dfrac{1}{{x - 1}} - \dfrac{2}{{{x^2} - 1}}\)
d) \(\dfrac{{x + 2}}{{{x^2} + xy}} - \dfrac{{y - 2}}{{xy + {y^2}}}\)
e) \(\dfrac{1}{{2{x^2} - 3x}} - \dfrac{1}{{4{x^2} - 9}}\)
g) \(\dfrac{{2x}}{{9 - {x^2}}} + \dfrac{1}{{x - 3}} - \dfrac{1}{{x + 3}}\)
Làm thế nào để cộng, trừ các phân thức đại số?
Thực hiện phép tính:
a) \(\dfrac{{5{\rm{x}} - 4}}{9} + \dfrac{{4{\rm{x}} + 4}}{9}\)
b) \(\dfrac{{{x^2}y - 6}}{{2{{\rm{x}}^2}y}} + \dfrac{{6 - x{y^2}}}{{2{{\rm{x}}^2}y}}\)
c) \(\dfrac{{x + 1}}{{{x^2} - 5{\rm{x}}}} + \dfrac{{x - 18}}{{{x^2} - 5{\rm{x}}}} + \dfrac{{x + 2}}{{{x^2} - 5{\rm{x}}}}\)
d) \(\dfrac{{7y}}{3} - \dfrac{{7y - 5}}{3}\)
e) \(\dfrac{{4{\rm{x}} - 1}}{{3{\rm{x}}{y^2}}} - \dfrac{{7{\rm{x}} - 1}}{{3{\rm{x}}{y^2}}}\)
g) \(\dfrac{{3y - 2{\rm{x}}}}{{x - 2y}} - \dfrac{{x - y}}{{2y - x}}\)
Thực hiện phép tính:
a) \(\dfrac{{4{{x}} + 2}}{{4{{x - 4}}}} + \dfrac{{3 - 6{{x}}}}{{6{{x}} - 6}}\)
b) \(\dfrac{y}{{2{{{x}}^2} - xy}} + \dfrac{{4{{x}}}}{{{y^2} - 2{{x}}y}}\)
c) \(\dfrac{x}{{x - y}} + \dfrac{y}{{x + y}} + \dfrac{{2{y^2}}}{{{x^2} - {y^2}}}\)
d) \(\dfrac{{{x^2} + 2}}{{{x^3} - 1}} + \dfrac{x}{{{x^2} + x + 1}} + \dfrac{1}{{1 - x}}\)
Thực hiện phép tính:
a) \(\frac{1}{{x - 2}} - \frac{1}{{x + 1}}\)
b) \(\frac{{12}}{{{x^2} - 9}} - \frac{2}{{x - 3}}\)
c) \(\frac{1}{{xy - {x^2}}} - \frac{1}{{{y^2} - xy}}\)
d) \(\frac{{2{\rm{x}}}}{{{x^2} - 1}} - \frac{3}{{2 + 2{\rm{x}}}} + \frac{1}{{2 - 2{\rm{x}}}}\)
a) Rút gọn biểu thức: \(A = \dfrac{{2{{\rm{x}}^2} + 1}}{{{x^3} + 1}} + \dfrac{{1 - x}}{{{x^2} - x + 1}} - \dfrac{1}{{x + 1}}\)
b) Tính giá trị của A tại x = -3
So sánh hai biểu thức \(C = - \left( {\frac{1}{x} - \frac{1}{{x - 1}}} \right)\) và \(D = - \frac{1}{x} + \frac{1}{{x - 1}}.\)
Thực hiện các phép tính sau:
a) \(\frac{1}{{2x - 3}} - \frac{2}{{3 - 2x}} + \frac{{18}}{{9 - 4{x^2}}}\)
b) \(\frac{2}{{{a^2} - 1}} - \frac{1}{{a + 1}} - \frac{1}{{a - 1}}\)
c) \(\frac{{a + b}}{{a - b}} + \frac{{{a^2} - 4{b^2}}}{{{a^2} - {b^2}}} - \frac{{a - 3b}}{{a + b}}\)
d) \(\frac{x}{{{x^2} + xy}} - \frac{y}{{{x^2} - {y^2}}} + \frac{{x + y}}{{xy - {y^2}}}\)
Tính nhanh \(\left( {\frac{y}{{x + z}} - \frac{y}{{x + y}} + \frac{{x + y}}{{x + y + z}}} \right) - \left( {\frac{y}{{x + z}} - \frac{z}{{x + y + z}} + \frac{x}{{x + y}}} \right).\)
Hãy trả lời các câu hỏi nêu trong phần khởi động:
Một xe ô tô đi từ thị trấn A đến thị trấn B (A và B cách nhau \(10\,km\)) với tốc độ trung bình là \(v\left( {km/h} \right)\). Một xe máy cũng đi từ A đến B với tốc độ trung bình chậm hơn \(10km/h\) so với tốc độ trung bình của ô tô. Hỏi tổng thời gian cả hai xe đi từ A đến B là bao nhiêu? Thời gian xe ô tô đi từ A đến B nhanh hơn thời gian xe máy đi từ A đến B là bao nhiêu?
Một đội máy xúc trên công trường nhận nhiệm vụ xúc \(17\,400\,{m^3}\) đất. Giai đoạn đầu, đội làm việc với năng suất trung bình \(x\,{m^3}\)/ngày và đào được \(7\,500\,{m^3}.\) Giai đoạn sau, năng suất của đội tăng \(25\,{m^3}\)/ngày.
a) Viết phân thức theo \(x\) biểu diễn thời gian để đội đó hoàn thành công việc.
b) Tính thời gian để đội đó hoàn thành công việc khi năng suất trung bình là \(250\,{m^3}\)/ngày.
Thực hiện các phép tính sau:
a) \(\frac{5}{{6x - 6}} + \frac{9}{{14x - 14}} + \frac{6}{{7x - 7}}\)
b) \(\frac{2}{{y - 4}} + \frac{1}{y} - \frac{3}{{y - 3}}\)
c) \(\frac{{8{a^2} + 18{b^2}}}{{4{a^2} - 9{b^2}}} - \frac{{2a + 3b}}{{2a - 3b}} + \frac{{2a - 3b}}{{2a + 3b}}\)
d) \(\frac{{a - 4}}{{2a - 1}} + \frac{{5{a^2} + 9a + 14}}{{2{a^2} + 3a - 2}} - \frac{{3a - 5}}{{a + 2}}\)
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\frac{x}{{x + 2}} - \frac{x}{{x - 2}}\);
b) \(\frac{{3x}}{{2y}} + \frac{{5x}}{{3y}}\);
c) \(\frac{{y - 1}}{{5y}} - \frac{{3x - 1}}{{15x}}\);
d) \(\frac{{1 - x}}{{{x^3}}} + \frac{1}{{{x^2}}}\);
e) \(\frac{{x - 2y}}{{x{y^2}}} - \frac{{y - 2x}}{{{x^2}y}}\);
g) \(\frac{{1 - {y^2}}}{{3xy}} + \frac{{2{y^3} - 1}}{{6x{y^2}}}\).
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\frac{b}{{a - b}} + \frac{{{a^2} - 3ab}}{{{a^2} - {b^2}}}\);
b) \(\frac{{a + 3}}{{{a^2} - 1}} - \frac{1}{{{a^2} + a}}\);
c) \(\frac{{2a}}{{{a^2} - 4a + 4}} + \frac{4}{{2 - a}}\);
d) \(\frac{{a + 1}}{{{a^3} - 1}} - \frac{1}{{{a^2} + a + 1}}\).
Tính:
a) \(x - \frac{{2x - y}}{4} + \frac{{x + 4y}}{{12}}\);
b) \(\frac{y}{x} - \frac{x}{y} - \frac{{{x^2} + {y^2}}}{{xy}}\);
c) \(\frac{4}{{x + 2}} - \frac{3}{{x - 2}} + \frac{{12}}{{{x^2} - 4}}\);
d) \(\frac{{x + y}}{{{x^2} - xy}} - \frac{{4x}}{{{x^2} - {y^2}}} - \frac{{x - y}}{{{x^2} + xy}}\).
Tính giá trị của biểu thức:
a) \(P = \frac{5}{{a + b}} + \frac{6}{{a - b}} - \frac{{12b}}{{{a^2} - {b^2}}}\) tại \(a = 0,12\) và \(b = - 0,11\);
b) \(Q = \frac{{{a^2} + 2a}}{{{a^3} - 1}} - \frac{1}{{{a^2} + a + 1}}\) tại \(a = 1,25\);
Tính:
a) \(\frac{1}{{ab}} + \frac{1}{{ac}} + \frac{1}{{bc}}\);
b) \(\frac{{b - a}}{{ab}} + \frac{{c - b}}{{bc}} - \frac{{c - a}}{{ac}}\).
Cô Xuân đi bộ quãng đường dài 3km với tốc độ trung bình x (km/h). Sau đó, cô đi tiếp quãng đường dài 2km với tốc độ trung bình \(x - 1\left( {km/h} \right)\). Tính tổng thời gian mà cô Xuân đã đi bộ theo x.







Danh sách bình luận