Cho ba đa thức \(P\left( x \right) = 3{x^4} - 2{x^2} + 8x - 10\); \(Q\left( x \right) = 4{x^3} - 6{x^2} + 7x - 1\) và \(R\left( x \right) = - 3{x^4} + 5{x^2} - 8x - 5\). Tính \(P\left( x \right) + Q\left( x \right) + R\left( x \right)\) và \(P\left( x \right) - Q\left( x \right) - R\left( x \right)\).
Bước 1: Thực hiện cộng trừ các đơn thức cùng một biến để rút gọn đa thức đã cho.
Bước 2: Sắp xếp các đơn thức theo lũy thừa giảm dần của biến.
Bước 3: Thực hiện phép tính theo hàng ngang hoặc cột dọc.
\(\begin{array}{*{20}{c}}{}&{3{x^4}}&{}&{}& - &{2{x^2}}& + &{8x}& - &{10}\\ + &{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{}&{}&{4{x^3}}& - &{6{x^2}}& + &{7x}& - &1\\ + &{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{ - 3{x^4}}&{}&{}& + &{5{x^2}}& - &{8x}& - &5\\\hline{}&{}&{}&{4{x^3}}& - &{3{x^2}}& + &{7x}& - &{16}\end{array}\)
Vậy \(P\left( x \right) + Q\left( x \right) + R\left( x \right) = 4{x^3} - 3{x^2} + 7x - 16\)
\(\begin{array}{*{20}{c}}{}&{3{x^4}}&{}&{}& - &{2{x^2}}& + &{8x}& - &{10}\\ - &{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{}&{}&{4{x^3}}& - &{6{x^2}}& + &{7x}& - &1\\ - &{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{ - 3{x^4}}&{}&{}& + &{5{x^2}}& - &{8x}& - &5\\\hline{}&{6{x^4}}& - &{4{x^3}}& - &{{x^2}}& + &{9x}& - &4\end{array}\)
Vậy \(P\left( x \right) - Q\left( x \right) - R\left( x \right) = 6{x^4} - 4{x^3} - {x^2} + 9x - 4\).

Các bài tập cùng chuyên đề
Tìm tổng của hai đa thức: x3 – 5x + 2 và x3 – x2 +6x – 4.
Cho hai đa thức M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5
Hãy tính tổng M + N ( trình bày theo 2 cách)
Đặt tính cộng để tìm tổng của ba đa thức sau:
A = 2x3 – 5x2 + x – 7
B = x2 – 2x + 6
C = -x3 + 4x2 - 1
Tìm tổng của hai đa thức sau bằng cách nhóm các hạng tử cùng bậc:
x2 – 3x + 2 và 4x3 – x2 + x - 1
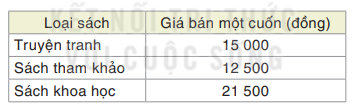
Bạn Nam được phân công mua một số sách làm quà tặng trong buổi tổng kết cuối năm học của lớp. Nam dự định mau ba loại sách với giá bán như bảng sau. Giả sử Nam cần mua x cuốn sách khoa học, x+8 cuốn sách tham khảo và x + 5 cuốn truyện tranh.
a) Viết các đa thức biểu thị số tiền Nam phải trả cho từng loại sách.
b) Tìm đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó.
Hai bạn Tròn và Vuông tranh luận với nhau như sau:
Hãy cho biết ý kiến của em và nêu một ví dụ minh họa.
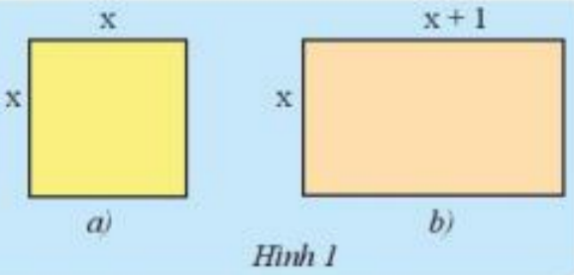
Hãy lập biểu thức biểu thị tổng chu vi hình vuông (Hình 1a) và hình chữ nhật (Hình 1b).
Cho hai đa thức P(x) = \(7{x^3} - 8x + 12\) và Q(x) = \(6{x^2} - 2{x^3} + 3x - 5\). Hãy tính P(x) + Q(x) bằng hai cách.
Thực hiện phép tính \((x - 4) + \left[ {({x^2} + 2x) + (7 - x)} \right]\)
Cho đa thức A(y) = \( - 5{y^4} - 4{y^2} + 2y + 7\)
Tìm đa thức B(y) sao cho B(y) – A(y) = \(2{y^3} - 9{y^2} + 4y\)
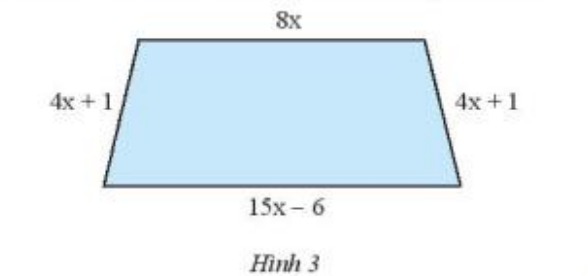
Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 3.
Cho đa thức \(P(x) = {x^3} - 4{x^2} + 8x - 2\). Hãy viết P(x) thành tổng của hai đa thức bậc bốn
a) Thực hiện phép cộng trong mỗi trường hợp sau: \(5{x^2} + 7{x^2}\); \(a{x^2} + b{x^2}\) (k \(\in\) N*).
b) Nêu quy tắc cộng hai đơn thức có cùng số mũ của biến.
Cho hai đa thức
\(P(x) = 5{x^2} + 4 + 2x\) và \(Q(x) = 8x + {x^2} + 1\).
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi cộng hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
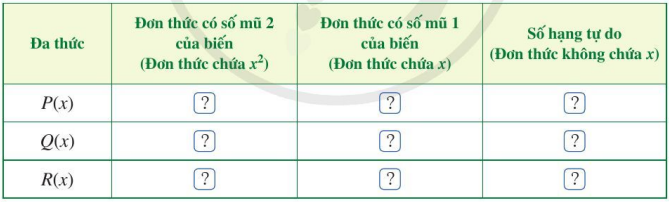
c) Dựa vào kết quả cộng hai đơn thức theo từng cột, xác định đơn thức R(x).
Để cộng hai đa thức P(x), Q(x), bạn Dũng viết như dưới đây có đúng không? Vì sao? Nếu chưa đúng, em hãy sửa lại cho đúng.
Cho hai đa thức:
\(P(x) = - 2{x^2} + 1 + 3x\) và \(Q(x) = - 5x + 3{x^2} + 4\).
a) Sắp xếp các đa thức P(x) và Q(x) theo số mũ giảm dần của biến.
b) Viết tổng P(x) + Q(x) theo hàng ngang.
c) Nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Tính tổng P(x) + Q(x) bằng cách thực hiện phép tính trong từng nhóm.
Tính tổng của hai đa thức sau bằng hai cách:
\(P(x) = 2{x^3} + \dfrac{3}{2}{x^2} + 5x - 2\);
\(Q(x) = - 8{x^3} + 4{x^2} + 6 + 3x\).
Bác Ngọc gửi ngân hàng thứ nhất 90 triệu đồng với kì hạn 1 năm, lãi suất x%/năm. Bác Ngọc gửi ngân hàng thứ hai 80 triệu đồng với kì hạn 1 năm, lãi suất \((x + 1,5)\)%/năm. Hết kì hạn 1 năm, bác Ngọc có được cả gốc lẫn lãi là bao nhiêu:
a) Ở ngân hàng thứ hai?
b) Ở cả hai ngân hàng?
Cho hai đa thức \(A\left( x \right) = x - 2{x^2} + 3{x^5} + {x^4} + x + {x^2}\); \(B\left( x \right) = - 2{x^2} + x - 2 - {x^4} + 3{x^2} - 3{x^5}\).
Tìm đa thức \(M(x)\) sao cho \(B(x) = A(x) + M(x)\). Tìm bậc và hệ số cao nhất của đa thức \(M(x)\).
Gọi S(x) là tổng của hai đa thức A(x) và B(x). Biết rằng x = a là một nghiệm của đa thức A(x). Chứng minh rằng:
a) Nếu x = a là một nghiệm của B(x) thì a cũng là một nghiệm của S(x).
b) Nếu a không là nghiệm của B(x) thì a cũng không là nghiệm của S(x).
Cho đa thức \(P\left( x \right) = - 3{x^2} + 7x - 5\). Hãy viết \(P\left( x \right)\) thành tổng của hai đa thức bậc bốn.
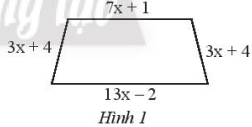
Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 1.
Số lượng xe du lịch được bán ra tại một nước từ năm 1983 tới năm 1996 được mô tả theo công thức \(C = - 0,016{t^4} + 0,49{t^3} - 4,8{t^2} + 14t + 70\) (tính bằng đơn vị nghìn chiếc), trong khi đó số xe tải thì tính theo \(T = - 0,01{t^4} + 0,31{t^3} - 3{t^2} + 11t + 23\), với t là số năm tính từ 1983. Viết biểu thức biểu thị số xe (cả xe du lịch và xe tải) được bán ra trong khoảng thời gian nêu trên. Tính số xe được bán ra vào năm 1990 (ứng với \(t = 7\)).
Cho hai đa thức: \(F(x) = {x^4} + {x^3} - 3{x^2} + 2x - 9\) và \(G(x) = - {x^4} + 2{x^2} - x + 8\)
a) Tìm đa thức H(x) sao cho H(x) = F(x) + G(x)
b) Tìm bậc của đa thức H(x)
c) Kiểm tra xem x = 0, x = 1, x = −1 có là nghiệm của đa thức H(x) hay không
d) Tìm đa thức K(x) sao cho H(x) - K(x) = \(\frac{1}{2}{x^2}\)
Mỗi chiếc bút bi được bán với giá x (đồng). Mỗi kẹp tóc có giá đắt hơn mỗi chiếc bút bi là 7 000 đồng, mỗi quyển truyện tranh có giá đắt gấp 5 lần mỗi chiếc bút bi. Bạn Khanh mua 4 chiếc kẹp tóc và 5 chiếc bút bi. Bạn Dung mua 1 quyển truyện tranh, 3 chiếc kẹp tóc và 10 chiếc bút bi.
a) Tính số tiền mỗi bạn phải trả theo x.
b) Tính tổng số tiền mà cửa hàng nhận được từ hai bạn Khanh và Dung theo x.
c) Nếu bạn Minh chỉ có 70 000 đồng và muốn mua hàng sao cho có đủ cả ba món đồ (bút bi, kẹp tóc, truyện tranh) thì bạn Minh có thể mua được nhiều nhất bao nhiêu chiếc kẹp tóc, biết giá mỗi chiếc bút bi là 5 000 đồng?
Cho hai đa thức P và Q sao cho cả ba đa thức P, Q, \(P + Q\) đều khác đa thức không. Khi đó luôn xảy ra
A. Bậc của \(P + Q\) lớn hơn bậc của P và của Q.
B. Bậc của \(P + Q\) nhỏ hơn bậc của P và của Q.
C. Bậc của \(P + Q\) bằng bậc của P hoặc bằng bậc của Q.
D. Bậc của \(P + Q\) bằng bậc của P nếu bậc của P lớn hơn bậc của Q.
Tìm tổng của hai đa thức sau bằng cách nhóm các hạng tử cùng bậc:
\({x^2} - 3x + 2\) và \(4{x^3} - {x^2} + x - 1\).
Bạn Nam được phân công mua một số sách làm quà tặng trong buổi tổng kết cuối năm học của lớp. Nam dự định mua ba loại sách với giá bán như bảng sau. Giả sử Nam cần mua x cuốn sách khoa học, \(x + 8\) cuốn sách tham khảo và \(x + 5\) cuốn truyện tranh.

a) Viết các đa thức biểu thị số tiền Nam phải trả cho từng loại sách.
b) Tìm đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó.
\(M\left( x \right) = - 5{x^4} + 3{x^5} + x\left( {{x^2} + 5} \right) + 14{x^4} - 6{x^5} - {x^3} + x - 1\); \(N\left( x \right) = {x^4}\left( {x - 5} \right) - 3{x^3} + 3x + 2{x^5} - 4{x^4} + 3{x^3} - 5\).
a) Tính \(H\left( x \right) = M\left( x \right) + N\left( x \right)\).
b) Tìm nghiệm của đa thức \(H\left( x \right)\).


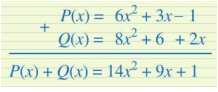






Danh sách bình luận