Trong quá trình rơi tự do của viên bi sắt thi tốc độ của nó
-
A.
giảm đi.
-
B.
không thay đồi.
-
C.
lúc đâu không thay đôi, về sau giam đi.
-
D.
tăng lên.
Dựa vào lí thuyết vật rơi tự do
Trong quá trình rơi tự do của viên bi sắt thi tốc độ của nó tăng lên
Chọn D.
Đáp án : D

Các bài tập cùng chuyên đề
Các thí nghiệm (TN) sau đây sẽ giúp chúng ta kiểm tra dự đoán của mình về sự rơi trong không khí.
TN 1: Thả rơi một quả bóng và một chiếc lá.
TN 2: Thả rơi tờ giấy giống nhau, nhưng một tờ được vo tròn, một tờ để nguyên.
TN 3: Thả rơi hai viên bi có cùng kích thước, một bằng sắt và một bằng thủy tinh.
Từ những thí nghiệm trên, rút ra nhận xét về sự rơi trong không khí.
1. Trong TN 1, tại sao quả bóng rơi nhanh hơn chiếc lá?
2. Trong TN 2, hai tờ giấy giống nhau, nặng như nhau, tại sao tờ giấy vo tròn lại rơi nhanh hơn?
3. Trong TN 3, trọng lượng bi sắt lớn hơn bi thủy tinh, tại sao hai viên bi rơi nhanh như nhau?
Trong các chuyển động sau, chuyển động nào được coi là rơi tự do? Tại sao?
A. Chiếc lá đang rơi
B. Hạt bụi chuyển động trong không khí
C. Quả tạ rơi trong không khí
D. Vận động viên đang nhảy dù
1. Hãy thực hiện thí nghiệm (Hình 10.2) để kiểm tra dự đoán về phương và chiều của sự rơi tự do.
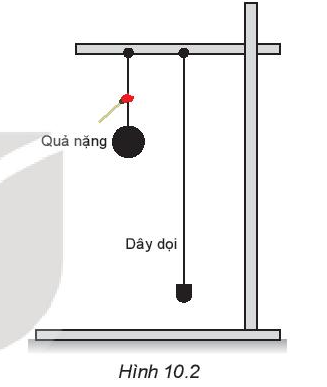
2. Dựa vào đặc điểm về phương của sự tự do, hãy tìm cách kiểm tra bề mặt của bức tường trong lớp học có phải là mặt phẳng thẳng đứng không.
3. Hãy nghĩ cách dùng êke tam giác vuông cân và dây dọi để kiểm tra xem sàn lớp mình có phẳng hay không.
Hãy căn cứ vào số liệu trong bảng 10.1 để:
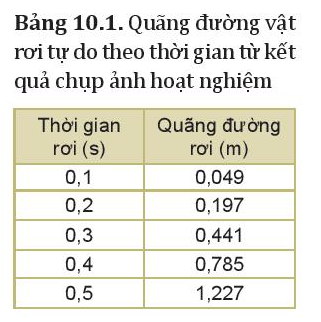
1. Chứng tỏ chuyển động rơi tự do là nhanh dần đều.
2. Tính gia tốc của chuyển động rơi tự do.
1. Tại sao độ dịch chuyển và quãng đường đi được trong sự rơi tự do có cùng độ lớn?
2. Hãy nêu cách đo gần đúng độ sâu của một cái giếng mỏ cạn. Coi vận tốc truyền âm trong không khí là không đổi và đã biết.
Một người thả rơi một hòn bi từ trên cao xuống đất và đo được thời gian rơi là 3,1 s. Bỏ qua sức cản không khí. Lấy g = 9,8 m/s2 .
a) Tính độ cao của nơi thả hòn bi so với mặt đất và vận tốc lúc chạm đất.
b) Tính quãng đường rơi được trong 0,5 s cuối trước khi chạm đất.
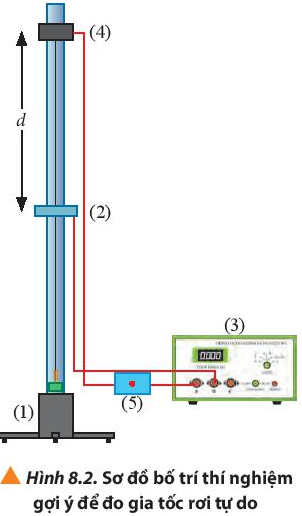
Thảo luận về phương án thí nghiệm dựa trên hoạt động sau: Thả trụ thép rơi qua cổng quang điện trên mảng đứng và trả lời câu hỏi.

1. Xác định gia tốc rơi tự do của trụ thép theo công thức nào?
2. Để xác định gia tốc rơi tự do của trụ thép cần đo đại lượng nào?
3. Làm thế nào để trụ thép rơi qua cổng quang điện?
4. Cần đặt chế độ đo của đồng hồ ở vị trí nào để đo được đại lượng cần đo?
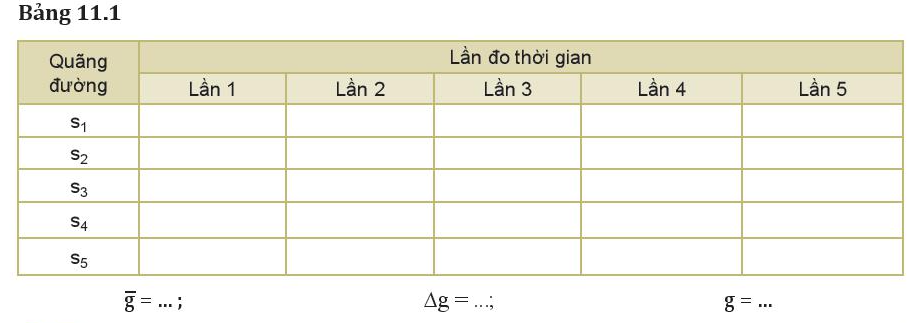
Nhận xét và đánh giá kết quả thí nghiệm:
1. Hãy tính giá trị trung bình và sai số tuyệt đối của phép đo gia tốc rơi tự do.
2. Tại sao lại dùng trụ thép làm vật rơi trong thí nghiệm? Có thể dùng viên bi thép được không? Giải thích tại sao.
3. Vẽ đồ thị mô tả mối quan hệ s và t2 trên hệ tọa độ (s – t2).
4. Nhận xét chung về dạng của đồ thị mô tả mối quan hệ s và t2 rồi rút ra kết luận về tính chất của chuyển động rơi tự do.
5. Hãy đề xuất một phương án thí nghiệm khác để đo gia tốc rơi tự do của trụ thép.
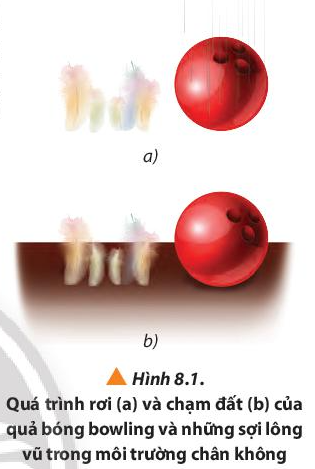
Vào năm 2014, Cơ quan hàng không và Vũ trụ Hoa Kỳ (NASA – National Aeronautics and Space Administration) đã thực hiện thí nghiệm thả rơi một quả bóng bowling và những sợi lông vũ trong phòng chân không từ cùng một độ cao. Kết quả cho thấy quả bóng bowling và những sợi lông vũ luôn chạm đất đồng thời như Hình 8.1. Tại sao lại như vậy?
Thực hiện thí nghiệm thả đồng thời một viên bi và một tờ giấy từ cùng một độ cao.
a) Nhận xét về thời gian di chuyển từ khi bắt đầu thả đến khi chạm đất của hai vật.
b) Hãy dự đoán trong điều kiện nào thì hai vật sẽ chạm đất đồng thời.
Dựa vào các kiến thức đã học và bộ dụng cụ gợi ý, các em hãy đề xuất một phương án đo gia tốc rơi tự do khác. Phân tích ưu, nhược điểm của phương án do em đề xuất so với phương án gợi ý
Dựa vào số liệu, lập luận để trình bày phương án và tiến hành xử lí số liệu để xác định gia tốc rơi tự do và sai số của phép đo.
Nêu ra các nguyên nhân gây ra sai số trong phương án thí nghiệm lựa chọn.
Dựa vào kết quả thí nghiệm, nhận xét về các tính chất của chuyển động rơi tự do.
Hãy tiến hành thí nghiệm đo gia tốc rơi tự do bằng cách sử dụng đồng hồ bấm giây hoặc các thiết bị khác như điện thoại thông minh. So sánh với kết quả được thực hiện tại phòng thí nghiệm và giá trị chính xác của gia tốc rơi tự do, nêu nhận xét và giải thích kết quả này.
Chuyển động của vật nào dưới đây sẽ được coi là rơi tự do nếu được thả rơi?
A. Một chiếc khăn voan nhẹ.
B. Một sợi chỉ.
C. Một chiếc lá cây rụng.
D. Một viên sỏi.
Chuyển động nào dưới đây có thể coi như là chuyển động rơi tự do?
A. Chuyển động của một viên bi sắt được ném theo phương nằm ngang.
B. Chuyển động của một viên bi sắt được ném theo phương xiên góc.
C. Chuyển động của một viên bi sắt được thả rơi.
D. Chuyển động của một viên bi sắt được ném lên cao.
Thả một hòn sỏi từ độ cao h xuống đất. Hòn sỏi rơi trong 2s. Nếu thả hòn sỏi từ độ cao 2h xuống đất thì hòn sỏi sẽ rơi trong bao lâu?
A. 2 s. B. \(2\sqrt 2 \)s. C. 4 s. D. \(4\sqrt 2 \)s.
Thả vật rơi tự do từ độ cao h xuống đất. Công thức tính vận tốc của vật khi chạm đất là:
A. v = \(2\sqrt {gh} .\) B. v = \(\sqrt {2gh} .\)
C. v = \(\sqrt {gh} .\) D. \(\sqrt {\frac{{gh}}{2}} .\)
Một vật được thả rơi tự do từ độ cao 9,8 m xuống đất. Bỏ qua lực cản của không khí. Lấy gia tốc rơi tự do g = 9,8 m/s2. Vận tốc v của vật trước khi chạm đất bằng
A. 9,8\(\sqrt 2 \) m/s. B. 9,8 m/s. C. 98 m/s. D. 6,9 m/s.
Hai vật được thả rơi tự do đồng thời từ hai độ cao khác nhau h1 và h2. Khoảng thời gian rơi của vật thứ nhất gấp đôi thời gian rơi của vật thứ hai. Bỏ qua lực cản của không khí. Tỉ số các độ cao h là:
A. \(\frac{{{h_1}}}{{{h_2}}} = 2\).
B. \(\frac{{{h_1}}}{{{h_2}}} = 0.5.\)
C. \(\frac{{{h_1}}}{{{h_2}}} = 4.\)
D. \(\frac{{{h_1}}}{{{h_2}}} = 1.\)
Tính khoảng thời gian rơi tự do t của một viên đá. Cho biết trong giây cuối cùng trước khi chạm đất, vật đã rơi được đoạn đường dài 24,5 m. Lấy gia tốc rơi tự do g = 9,8 m/s2.
Tính quãng đường mà vật rơi tự do đi được trong giây thứ tư kể từ lúc được thả rơi. Trong khoảng thời gian đó vận tốc của vật đã tăng lên bao nhiêu? Lấy gia tốc rơi tự do g= 9,8 m/s2.
Thả một hòn đá rơi từ miệng một cái hang sâu xuống đến đáy. Sau 4 s kể từ lúc bắt đầu thả thì nghe tiếng hòn đá chạm vào đáy. Tính chiều sâu của hang. Biết vận tốc truyền âm trong không khí là 330 m/s. Lấy g = 9,8m/s2.
Thả một hòn sỏi từ trên gác cao xuống đất. Trong giây cuối cùng hòn sỏi rơi được quãng đường 15 m. Tính độ cao của điểm từ đó bắt đầu thả rơi hòn sỏi. Lấy g = 9,8m/s2.
Quả bóng được thả từ độ cao 1,2 m. Sau khi chạm đất, nó nảy lên tới độ
cao 0,8 m. Thời gian bóng tiếp xúc với mặt đất giữa B và D là 0,16 s (Vì thời gian này quá nhỏ nên trong hình vẽ đã bỏ qua). Coi sức cản của không khi là không đáng kể, lấy g = 10 m/s2.
a) Tính vận tốc của quả bóng ngay trước khi tiếp đất và ngay sau khi nảy lên.
b) Tính gia tốc của quả bóng trong thời gian tiếp xúc với đất.
Một cầu thủ tennis ăn mừng chiến thắng bằng cách đánh quả bóng lên trời theo phương thẳng đứng với vận tốc lên tới 30 m/s. Bỏ qua sức cản của không khí và lấy g =10 m/s2.
a) Tính độ cao cực đại mà bóng đạt được.
b) Tính thời gian từ khi bóng đạt độ cao cực đại tới khi trở về vị trí được đánh lên.
c) Tính vận tốc của bóng ở thời điểm t = 5s kể từ khi được đánh lên.
d) Vẽ đồ thị vận tốc - thời gian và gia tốc - thời gian của chuyển động của bóng.
Một quả bóng quần vợt được thả ra từ một khinh khí cầu đang bay lên theo phương thẳng đứng với vận tốc 7,5 m/s. Bóng rơi chạm đất sau 2,5 s. Bỏ qua sức cản của không khí và lấy g = 10 m/s2.
a) Mô tả chuyển động của bóng.
b) Vẽ đồ thị vận tốc - thời gian của bóng.
c) Xác định thời điểm bóng đạt độ cao cực đại.
d) Tính quãng đường đi được của bóng từ khi được thả ra tới khi đạt độ cao
cực đại.
e) Độ cao cực đại của bóng cách mặt đất bao nhiêu?






