Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình \(x - 3y - z + 8 = 0\). Vecto nào sau đây là một vecto pháp tuyến của mặt phẳng (P)?
-
A.
\(\overrightarrow {{n_1}} (1; - 3;1)\)
-
B.
\(\overrightarrow {{n_2}} (1; - 3; - 1)\)
-
C.
\(\overrightarrow {{n_3}} (1; - 3;8)\)
-
D.
\(\overrightarrow {{n_4}} (1;3;8)\)
Phương trình mặt phẳng có dạng tổng quát là \(Ax + By + Cz + D = 0\) với \(\vec n(A;B;C)\) là một vecto pháp tuyến của mặt phẳng.
Mặt phẳng (P): \(x - 3y - z + 8 = 0\) có vecto pháp tuyến là \(\vec n(1; - 3; - 1)\).
Đáp án : B

Các bài tập cùng chuyên đề
Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2;3} \right),B\left( { - 3;0;1} \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB. Hãy chỉ ra một vectơ pháp tuyến của \(\left( \alpha \right)\).
Moment lực là một đại lượng Vật lí, thể hiện tác động gây ra sự quay quanh một điểm hoặc một trục của một vật thể. Trong không gian Oxyz, với đơn vị đo là mét, nếu tác động vào cán mỏ lết tại vị trí P một lực \(\overrightarrow F \) để vặn con ốc ở vị trí O (H.5.6) thì moment lực \(\overrightarrow M \) được tính bởi công thức \(\overrightarrow M = \left[ {\overrightarrow {OP} ,\overrightarrow F } \right]\).
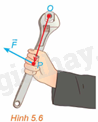
a) Cho \(\overrightarrow {OP} = \left( {x;y;z} \right),\overrightarrow F = \left( {a;b;c} \right)\), Tính \(\overrightarrow M \).
b) Giải thích vì sao, nếu giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi. Từ đó, ta có thể rút ra điều gì để đỡ tốn sức khi dùng mỏ lết vặn ốc?
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1; - 2;1} \right),B\left( { - 2;1;0} \right),C\left( { - 2;3;2} \right)\). Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (ABC).
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P).
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của nó có vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) hay không?
b) Mặt phẳng (P) có nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến hay không?
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {2;3;1} \right)\) và \(\overrightarrow v = \left( {4;6;2} \right)\). Tính \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
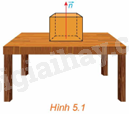
Trên mặt bàn phẳng, đặt một vật. Khi đó, mặt bàn tác động lên vật phản lực pháp tuyến \(\overrightarrow n \), giá của vectơ \(\overrightarrow n \) vuông góc với mặt bàn. Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương gì? (H.5.1)
Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng.
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì?
Trong không gian Oxyz, cho điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và mặt phẳng \(\left( P \right):Ax + By + Cz + D = 0\) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\). Gọi N là hình chiếu vuông góc của M trên (P). (H.5.13)
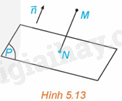
a) Giải thích vì sao tồn tại số k để \(\overrightarrow {MN} = k\overrightarrow n \). Tính tọa độ của N theo k, tọa độ của M và các hệ số A, B, C, D.
b) Thay tọa độ của N vào phương trình mặt phẳng (P) để từ đó tính k theo tọa độ của M và các hệ số A, B, C, D.
c) Từ \(\left| {\overrightarrow {MN} } \right| = \left| k \right|\left| {\overrightarrow n } \right|\), hãy tính độ dài của đoạn thẳng MN theo tọa độ của M và các hệ số A, B, C, D. Từ đó suy ra công thức tính khoảng cách từ điểm M đến mặt phẳng (P).
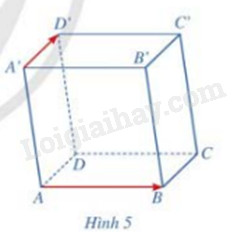
Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vecto \(\overrightarrow {AA'} \) có vuông góc với mặt phẳng (ABCD) hay không?
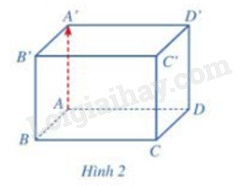
Cho cặp vecto chỉ phương \(\overrightarrow a = (1;0;1),\overrightarrow b = (2;1;0)\) của mặt phẳng (P).
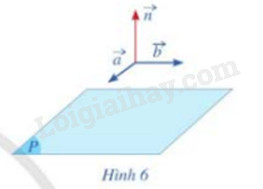
a) Hãy chỉ ra tọa độ của một vecto \(\overrightarrow n (\overrightarrow n \ne \overrightarrow 0 )\) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) (Hình 6)
b) Vecto \(\overrightarrow n \) có là vecto pháp tuyến của mặt phẳng (P) hay không?
Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)
Mặt phẳng \(x + 2y - 3z + 4 = 0\) có một vecto pháp tuyến là:
A. \(\overrightarrow {{n_1}} = (2; - 3;4)\)
B. \(\overrightarrow {{n_2}} = (1;2;3)\)
C. \(\overrightarrow {{n_3}} = (1;2; - 3)\)
D. \(\overrightarrow {{n_4}} = (1;2;4)\)
a) Cho vectơ \(\vec n\) khác \(\vec 0\). Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) vuông góc với giá của vectơ \(\vec n\)?
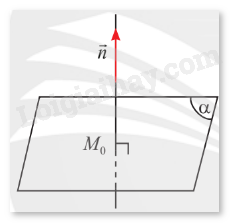
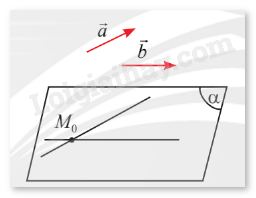
b) Cho hai vectơ \(\vec a\) và \(\vec b\) không cùng phương. Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\)?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;0;0} \right)\), \(B\left( {0;4;0} \right)\), \(C\left( {0;0;5} \right)\).
a) Tìm toạ độ của một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Tìm toạ độ của một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
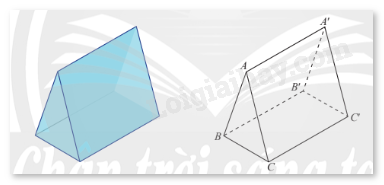
Một lăng kính có dạng hình trụ đứng có đáy là tam giác đều ở hình a được vẽ lại như hình b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) có cặp vectơ chỉ phương \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\), \(\vec b = \left( {{b_1};{b_2};{b_3}} \right)\). Xét vectơ \(\vec n = \left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} \right)\).
a) Vectơ \(\vec n\) có khác \(\vec 0\) hay không?
b) Tính \(\vec a.\vec n\); \(\vec b.\vec n\).
c) Vectơ \(\vec n\) có phải là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) không?
Cho mặt phẳng \(\left( Q \right)\) đi qua ba điểm \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;5} \right)\), \(C\left( {10;7; - 1} \right)\). Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của \(\left( Q \right)\).
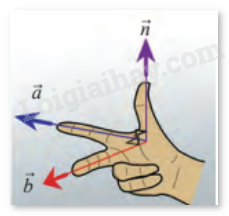
Cho biết hai vectơ \(\vec a = \left( {2;1;1} \right)\), \(\vec b = \left( {1; - 2;0} \right)\) có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong hình dưới đây. Tìm vectơ \(\vec n\) có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành 3 đường thẳng đôi một vuông góc).
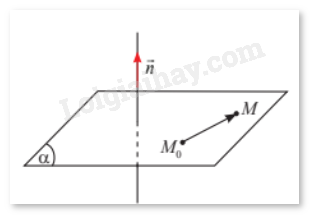
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {1;2;3} \right)\) và nhận \(\vec n = \left( {7;5;2} \right)\) làm vectơ pháp tuyến. Gọi \(M\left( {x;y;z} \right)\) là một điểm tuỳ ý trong không gian. Tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \) theo \(x,y,z\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) có phương trình \(Ax + By + Cz + D = 0\) và điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\). Gọi \({M_1}\left( {{x_1};{y_1};{z_1}} \right)\) là hình chiếu vuông góc của \({M_0}\) trên \(\left( \alpha \right)\)(hình dưới đây).
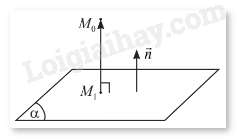
a) Nêu nhận xét về phương của hai vectơ \(\overrightarrow {{M_1}{M_0}} = \left( {{x_0} - {x_1};{y_0} - {y_1};{z_0} - {z_1}} \right)\) và \(\vec n = \left( {A;B;C} \right)\)
b) Tính \(\overrightarrow {{M_1}{M_0}} .\vec n\) theo \(A\), \(B\), \(C\), \(D\) và toạ độ của \({M_0}\).
c) Giải thích tại sao ta lại có đẳng thức \(\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|\).
d) Từ các kết quả trên suy ra cách tính \(d\left( {{M_0},\left( \alpha \right)} \right) = \left| {\overrightarrow {{M_1}{M_0}} } \right| = \frac{{\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right|}}{{\left| {\vec n} \right|}}\).
Cho mặt phẳng
\(\left( P \right):x + 2y + 3z - 1 = 0\). Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( P \right)\)?
A. \(\overrightarrow {{n_1}} = \left( {1;3; - 1} \right)\)
B. \(\overrightarrow {{n_2}} = \left( {2;3; - 1} \right)\)
C. \(\overrightarrow {{n_3}} = \left( {1;2; - 1} \right)\)
D. \(\overrightarrow {{n_4}} = \left( {1;2;3} \right)\)
Cho mặt phẳng \(\left( P \right): - x + 2y + 3 = 0\). Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \(\left( P \right)\)?
A. \(\overrightarrow {{n_1}} = \left( { - 1;2;3} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {1;2;3} \right)\).
C. \(\overrightarrow {{n_3}} = \left( { - 1;2;0} \right)\).
D. \(\overrightarrow {{n_4}} = \left( { - x;2y;3} \right)\).
Cho mặt phẳng \(\left( P \right):3x - 6y + 12z - 13 = 0\). Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \(\left( P \right)\)?
A. \(\overrightarrow {{n_1}} = \left( {3;6;12} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {3x;6y;12z} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {3x; - 6y;12z} \right)\).
D. \(\overrightarrow {{n_4}} = \left( { - 1;2; - 4} \right)\).
Cho mặt phẳng \(\left( P \right):3x + 4y - z + 5 = 0\). Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \(\left( P \right)\)?
A. \(\overrightarrow {{n_1}} = \left( {3;4;1} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {3;4; - 1} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {3;4;5} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {3;4; - 5} \right)\).
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Cho mặt phẳng \(\left( P \right): - 3x + y - 2z + 5 = 0\).
a) Nếu \(\overrightarrow n \) là một vectơ pháp tuyến của \(\left( P \right)\) thì \(k\overrightarrow n \) là một vectơ pháp tuyến của \(\left( P \right)\) với \(k \ne 0\).
b) Nếu \(\overrightarrow n \) và \(\overrightarrow {n'} \) đều là vectơ pháp tuyến của \(\left( P \right)\) thì \(\overrightarrow n \) và \(\overrightarrow {n'} \) không cùng phương.
c) Vectơ \(\overrightarrow n = \left( { - 3;1; - 2} \right)\) không là một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\).
d) Mọi vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) có toạ độ \(\left( { - 3k;k; - 2k} \right)\) với \(k \ne 0\).
Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \(\left( P \right): - x + 2y - 9z + 7 = 0\)?
A. \(\overrightarrow {{n_1}} = \left( {1;2;9} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {1; - 2;9} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {1;2; - 9} \right)\).
D. \(\overrightarrow {{n_4}} = \left( { - 1;2;9} \right)\).
Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \(\left( Q \right):5x - 6z + 4 = 0\)?
A. \(\overrightarrow {{n_1}} = \left( {5;0; - 6} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {5; - 6;4} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {5;0;6} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {5;6;4} \right)\).
Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \(\left( R \right):z - 2 = 0\)?
A. \(\overrightarrow {{n_1}} = \left( {1; - 2;0} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {1;0; - 2} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {0;0;1} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {1;2;0} \right)\).
Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng chứa đường thẳng
\(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = - 2 + 2t\\z = 3 - t\end{array} \right.\) và đi qua điểm \(A\left( {2; - 1;1} \right)\) là
A. \(\overrightarrow {{n_1}} = \left( {3; - 1;1} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {3;1; - 1} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {1; - 1;3} \right)\).
D. \(\overrightarrow {{n_4}} = \left( { - 1;3;1} \right)\).
Cho mặt phẳng \(\left( Q \right)\) nhận \(\overrightarrow a = \left( {4;0;1} \right);\overrightarrow b = \left( {2;1;1} \right)\) làm cặp vectơ chỉ phương. Tìm một vectơ pháp tuyến của \(\left( Q \right)\).







Danh sách bình luận