Từ độ cao \({y_0}\) mét, một quả bóng được ném lên xiên một góc \(\alpha \) so với phương ngang với vạn tốc đầu \({v_0}\) có phương trình chuyển động
\(y = \frac{{ - g}}{{2{v_0}^2{{\cos }^2}\alpha }}{x^2} + \left( {\tan \alpha } \right)x + {y_0}\) với \(g = 10\) m/s2
a) Viết phương trình chuyển động của quả bóng nếu \(\alpha = 30^\circ ,{y_0} = 2\) m và \({v_0} = 7\) m/s.
b) Để ném được quả bóng qua bức tường cao 2,5 m thì người ném phải đứng cách tường bao xa?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
a) Thay \(\alpha = 30^\circ ,{y_0} = 2\) m và \({v_0} = 7\) m/s vào phương trình chuyển động ta có:
\(y = \frac{{ - 10}}{{{{2.7}^2}{{\cos }^2}30^\circ }}{x^2} + \left( {\tan 30^\circ } \right)x + 2 = - \frac{{20}}{{147}}{x^2} + \frac{{\sqrt 3 }}{3}x + 2\)
b) Để ném quả bóng qua bước tường cao 2,5 mét thì \(y > 2,5 \Leftrightarrow - \frac{{20}}{{147}}{x^2} + \frac{{\sqrt 3 }}{3}x + 2 > 2,5 \Leftrightarrow - \frac{{20}}{{147}}{x^2} + \frac{{\sqrt 3 }}{3}x - 0,5 > 0\)
Tam thức bậc hai \( - \frac{{20}}{{147}}{x^2} + \frac{{\sqrt 3 }}{3}x - 0,5\) có a < 0 và hai nghiệm là \(x = \frac{{7\sqrt 3 }}{{10}}\) và \(x = \frac{{7\sqrt 3 }}{4}\)
Do đó \( - \frac{{20}}{{147}}{x^2} + \frac{{\sqrt 3 }}{3}x - 0,5 > 0 \Leftrightarrow x \in \left( {\frac{{7\sqrt 3 }}{{10}};\frac{{7\sqrt 3 }}{4}} \right)\)
\(\frac{{7\sqrt 3 }}{{10}} \approx 1,21;\frac{{7\sqrt 3 }}{4} \approx 3,03\)
Vậy người ném bóng cần đứng cách tường khoảng 1,21 m đến 3,03 m
Các bài tập cùng chuyên đề
Luyện tập – vận dụng 4 trang 53 SGK Toán 10 tập 1 – Cánh diều
Tổng chi phí T (đơn vị tính: nghìn đồng) để sản xuất Q sản phẩm được cho bởi biểu thức \(T = {Q^2} + 30Q + 3300\); giá bán của 1 sản phẩm là 170 nghìn đồng. Số sản phẩm được sản xuất trong khoảng nào để đảm bảo không bị lỗ (giả thiết các sản phẩm được bán hết)?
Xét hệ toạ độ Oth trên mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,2) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8,5 m sau 1 giây và đạt độ cao 6 m sau 2 giây.
a) Hãy tìm hàm số bậc hai biểu thị quỹ đạo chuyển động của quả bóng.
b) Trong khoảng thời gian nào thì quả bóng vẫn chưa chạm đất?
Công ty An Bình thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau:
10 khách đầu tiên có giá là 800 000 đồng/người. Nếu có nhiều hơn 10 người đăng kí thì cứ có thêm 1 người, giá vé sẽ giảm 10 000 đồng/người cho toàn bộ hành khách.
a) Gọi x là số lượng khách từ người thứ 11 trở lên của nhóm. Biểu thị doanh thu theo x.
b) Số người của nhóm khách du lịch nhiều nhất là bao nhiêu thì công ty không bị lỗ? Biết rằng chi phí thực sự cho chuyến đi là 700 000 đồng/người.
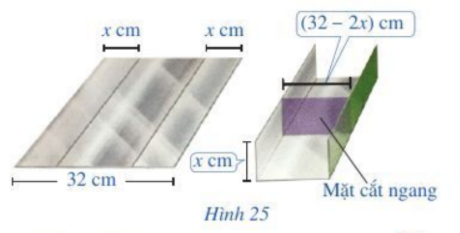
Bác Dũng muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 32 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông (Hình 25). Để đảm bảo kī thuật, diện tích mặt cắt ngang của rānh dẫn nước phải lớn hơn hoặc bằng 120 \(cm^2\). Rãnh dẫn nước phải có độ cao ít nhất là bao nhiêu xǎng-ti-mét?
Xét hệ tọa độ \(Oth\) trong mặt phẳng, trong đó trục \(Ot\) biểu thị thời gian \(t\) (tính bằng giây) và trục \(Oh\) biểu thị độ cao \(h\) (tính bằng mét). Một quả bóng được đá lên từ điểm \(A\left( {0;0,3} \right)\) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8m sau 1 giây, và đạt độ cao 6m sau 2 giây. Trong khoảng thời gian nào (tính bằng giây) thì quả bóng ở độ cao lơn hơn 5m và nhỏ hơn 7m (làm tròn kết quả đến hàng phần nghìn)?
Một tình huống trong huấn luyện pháo binh được mô tả như sau: Trong mặt phẳng tọa độ \(Oxy\) (đơn vị trên hai trục tính theo mét), một viên đạn được bắn từ vị trí \(O\left( {0;0} \right)\) theo quỹ đạo là đường parabol \(y = - \frac{9}{{1\;000\;000}}{x^2} + \frac{3}{{100}}x\). Tìm khoảng cách theo trục hoành của viên đạn so với vị trí bắn khi viên đạn đang ở độ cao lớn hơn 15m (làm tròn kết quả đến hàng phần trăm theo đơn vị mét).
Một người vay 100 triệu đồng tại một ngân hàng để mua nhà với lãi suất r%/năm trong thời hạn 2 năm. Hỏi số tiền người này phải trả cho ngân hàng là bao nhiêu triệu đồng sau 2 năm?
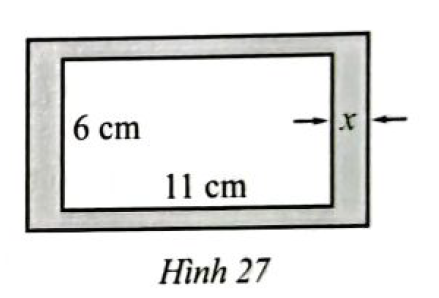
Bác Nam dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 6 cm x 11 cm, độ rộng viền xung quanh là \(x\) cm (Hình 27). Diện tích của viền khung ảnh không vượt quá \(38c{m^2}\). Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu cm?
Độ cao so với mặt đất của một quá bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai \(h(t) = - 4,9{t^2} + 20t + 1\), ở độ cao \(h(t)\)tính bằng mét và thời gian t tình bằng giây. Trong khoảng thời điểm nào trong quá trình bay của nó, quả bóng sẽ ở độ cao trên 5m so với mặt đất.
Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao 320 m với vận tốc ban đầu \({v_0} = 20m/s\). Hỏi sau ít nhất bao nhiêu giây, vật đó cách mặt đất không quá 100 m? Giả thiết rằng sức cản của không khí là không đáng kể.
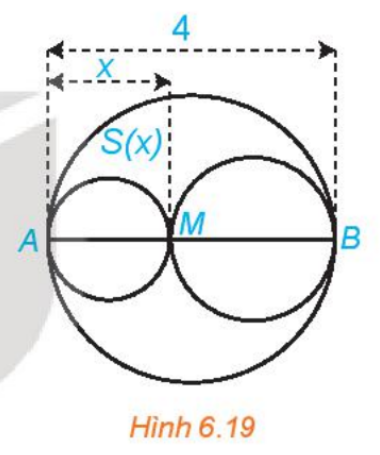
Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.
Kim muốn trồng một vườn hoa trên mảnh đất hình chữ nhật và làm hàng rào bao quanh. Kim chỉ có đủ vật liệu để làm 30 m hàng rào nhưng muốn diện tích vườn hoa ít nhất là 50 \({m^2}\). Hỏi chiều rộng của vườn hoa nằm trong khoảng nào?
Một quả bóng được ném thẳng đứng lên từ độ cao 1,6 m so với mặt đất với vận tốc là 10 m/s độ cao của bóng so với mặt đất (tính bằng mét) sau t giây được cho bởi hàm số \(h\left( t \right) = - 4,9{t^2} + 10t + 1,6\). Hỏi:
a) Bóng có thể cao trên 7 m không?
b) Bóng ở độ cao trên 5 m trong khoảng thời gian bao lâu? Làm tròn kết quả đến hàng phần trăm.
Mặt cắt ngang của mặt đường thường có hình dạng parabol để nước mưa dễ dàng thoát sang hai bên. Mặt cắt ngang của một con đường được mô tả bằng hàm số \(y = - 0,006{x^2}\) với gốc tọa độ đặt tại tim đường và đơn vị đo là mét như hình 4. Với chiều rộng của đường như thế nào thì thì tim đường cao hơn đường không quá 15 cm?
Một quả bóng được bắn thẳng lên từ độ cao 2 m với vận tốc ban đầu là 30 m/s. Khoảng cách quả bóng so với mặt đất t giây được cho bởi hàm số:
\(h\left( t \right) = - 4,9{t^2} + 30t + 2\)
với \(h\left( t \right)\) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 40 m trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.
Một chú cá heo nhảy lên khỏi mặt nước sau t giây được cho bởi hàm số \(h\left( t \right) = - 4,9{t^2} + 9,6t\).
Tính khoảng thời gian cá heo ở trên không.
Lợi nhuận một tháng \(p\left( x \right)\) của một quán ăn phụ thuộc vào giá trung bình x của các món ăn theo công thức \(p\left( x \right) = - 30{x^2} + 2100x - 15000\), với đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng nào?
Quỹ đạo của một quả bóng được mô tả bằng hàm số \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5\) với y (tính bằng mét) là độ cao của quả bóng so với mặt đất khi độ dịch chuyển theo phương ngang của bóng là x (tính bằng mét). Để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười.
Một công ti đồ gia dụng sản xuất bình đựng nước thấy rằng khi đơn giá của bình đựng nước là x nghìn đồng thì doanh thu R (tính theo đơn vị nghìn đồng) sẽ là \(R(x) = - 560{x^2} + 50000x\).
a) Theo mô hình doanh thu này, thì đơn giá nào là quá cao dẫn đến doanh thu từ việc bán bình đựng nước bằng 0 (tức là sẽ không có người mua)?
b) Với khoảng đơn giá nào của bình đựng nước thì doanh thu từ việc bán bình đựng nước vượt mức 1 tỉ đồng?
Một viên đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu 500 m/s, hợp với phương ngang một góc bằng 450. Biết rằng khi bỏ qua sức cản của không khí, quỹ đạo chuyển động của một vật ném xiên sẽ tuân theo phương trình:
\(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \)
trong đó x là khoảng cách (tính bằng mét) vật bay được theo phương ngang, vận tốc ban đầu v0 của vật hợp với phương ngang một góc \(\alpha \) và g = 9,8 m/s2 là gia tốc trọng trường.
a) Viết phương trình chuyển động của viên đạn
b) Để viên đạn bay qua một ngọn núi cao 4 000 mét thì khẩu pháp phải đặt cách chân núi một khoảng bao xa?
Cho a, b, c là độ dài 3 cạnh của một tam giác. Chứng minh rằng:
\({b^2}{x^2} - ({b^2} + {c^2} - {a^2})x + {c^2} > 0,\forall x \in \mathbb{R}\).
Một quả bóng được nắm thẳng lên từ độ cao \({h_{_0}}\)(m) với vận tốc \({v_0}\) (m/s). Độ cao của bóng so với mặt đất (tính bằng mét) sau t (s) được cho bởi hàm số
\(h\left( t \right) = - \frac{1}{2}g{t^2} + {v_0}t + {h_0}\) với \(g = 10\) (m/s2) là gia tốc trọng tường.
a) Tính \({h_{_0}}\) và \({v_0}\) biết độ cao của quả bóng sau 0,5 giây và 1 giây lần lượt là 4,75 m và 5 m.
b) Quả bóng có thể đạt được độ cao trên 4 m không? Nếu có thì trong thời gian bao lâu?
c) Cúng ném từ độ cao \({h_{_0}}\) như trên, nếu muốn độ cao của bóng sau 1 giây trong khoảng từ 2 m đến 3 m thì vận tốc ném bóng \({v_0}\) cần là bao nhiêu?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Lợi nhuận thu được từ việc sản xuất và bán x sản phẩm thủ công của một cửa hàng là:
\(I\left( x \right) = - 0,1{x^2} + 235x - 70000\)
Với I được tính bằng đơn vị nghìn đồng. Với số lượng sản phẩm bán ra là bao nhiêu thì cửa hàng có lãi?
Một hình chữ nhật có chu vi bằng 20 cm. Để tính diện tích hình chữ nhật lớn hơn hoặc bằng 15 cm2 thì chiều rộng của hình chữ nhật nằm trong khoảng bao nhiêu?
Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m.
a) Chọn trục hoành là đường thẳng nối hai chân cổng, gốc tọa độ tại một chân cổng, chân cổng còn lại có hoành độ dương, đơn vị là 1 m. Hãy viết phương trình của vòm cổng.
b) Người ta cần chuyền một thùng hàng hình hộp chữ nhật với chiều cao 3 m. Chiều rộng của thùng hàng tối đa là bao nhiêu để thùng có thể chuyển lọt qua được cổng?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Bộ phận nghiên cứu thị trường của một xí nghiệp xác định tổng chi phí để sản xuất Q sản phẩm là \({Q^2} + 300Q + 20000\) (nghìn đồng). Giả sử mỗi sản phẩm bán ra thị trường là 1200 nghìn đồng. Xí nghiệp cần sản xuất số sản phẩm ít nhất bằng a và nhiều nhất bằng b để không bị lỗ. Tính a + b.
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách nhau sau: 50 khách đầu tiên có giá 300000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm 1 người, giá vé sẽ giảm 5000 đồng/người cho toàn bộ hành khách. Biết chi phí thực sự của chuyến đi là 15080000 đồng. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu để công ty không bị lỗ?
